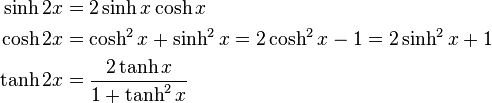Hyperbolic Function - Comparison With Circular Trigonometric Functions

Comparison With Circular Trigonometric Functions

Consider these two subsets of the Cartesian plane

Then A forms the right branch of the unit hyperbola {(x,y): x2 − y2 = 1}, while B is the unit circle. Evidently = {(1, 0)}. The primary difference is that the map t → B is a periodic function while t → A is not.

There is a close analogy of A with B through split-complex numbers in comparison with ordinary complex numbers, and its circle group. In particular, the maps t → A and t → B are the exponential map in each case. They are both instances of one-parameter groups in Lie theory where all groups evolve out of the identity For contrast, in the terminology of topological groups, B forms a compact group while A is non-compact since it is unbounded.

The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric identities. In fact, Osborn's rule states that one can convert any trigonometric identity into a hyperbolic identity by expanding it completely in terms of integral powers of sines and cosines, changing sine to sinh and cosine to cosh, and switching the sign of every term which contains a product of 2, 6, 10, 14, ... sinhs. This yields for example the addition theorems

\begin{align} \sinh(x + y) &= \sinh (x) \cosh (y) + \cosh (x) \sinh (y) \\ \cosh(x + y) &= \cosh (x) \cosh (y) + \sinh (x) \sinh (y) \\ \tanh(x + y) &= \frac{\tanh (x) + \tanh (y)}{1 + \tanh (x) \tanh (y)} \end{align}

the "double argument formulas"

\begin{align} \sinh 2x &= 2\sinh x \cosh x \\ \cosh 2x &= \cosh^2 x + \sinh^2 x = 2\cosh^2 x - 1 = 2\sinh^2 x + 1 \\ \tanh 2x &= \frac{2\tanh x}{1 + \tanh^2 x} \end{align}

and the "half-argument formulas"

Note: This is equivalent to its circular counterpart multiplied by −1.
Note: This corresponds to its circular counterpart.

The derivative of sinh x is cosh x and the derivative of cosh x is sinh x; this is similar to trigonometric functions, albeit the sign is different (i.e., the derivative of cos x is −sin x).

The Gudermannian function gives a direct relationship between the circular functions and the hyperbolic ones that does not involve complex numbers.

The graph of the function a cosh(x/a) is the catenary, the curve formed by a uniform flexible chain hanging freely between two fixed points under uniform gravity.

Read more about this topic:  Hyperbolic Function

Famous quotes containing the words comparison with, comparison, circular and/or functions:

    “Clay answered the petition by declaring that while he looked on the institution of slavery as an evil, it was ‘nothing in comparison with the far greater evil which would inevitably flow from a sudden and indiscriminate emancipation.’”
    —State of Indiana, U.S. public relief program (1935-1943)

    “He was a superior man. He did not value his bodily life in comparison with ideal things. He did not recognize unjust human laws, but resisted them as he was bid. For once we are lifted out of the trivialness and dust of politics into the region of truth and manhood.”
    —Henry David Thoreau (1817–1862)

    “If one doubts whether Grecian valor and patriotism are not a fiction of the poets, he may go to Athens and see still upon the walls of the temple of Minerva the circular marks made by the shields taken from the enemy in the Persian war, which were suspended there. We have not far to seek for living and unquestionable evidence. The very dust takes shape and confirms some story which we had read.”
    —Henry David Thoreau (1817–1862)

    “Adolescents, for all their self-involvement, are emerging from the self-centeredness of childhood. Their perception of other people has more depth. They are better equipped at appreciating others’ reasons for action, or the basis of others’ emotions. But this maturity functions in a piecemeal fashion. They show more understanding of their friends, but not of their teachers.”
    —Terri Apter (20th century)