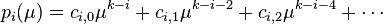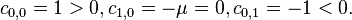Hopf Bifurcation - Example

Example

Let us consider the classical Van der Pol oscillator written with ordinary differential equations:

\left \{ \begin{array}{l} \dfrac{dx}{dt} = \mu (1-y^2)x - y, \\ \dfrac{dy}{dt} = x. \end{array} \right .

The Jacobian matrix associated to this system follows:

J = \begin{pmatrix} -\mu (-1+y^2) & -2 \mu y x -1 \\ 1 & 0 \end{pmatrix}.

The characteristic polynomial (in ) of the linearization at (0,0) is equal to:

P(\lambda) = \lambda^2 - \mu \lambda + 1.

The coefficients are:
The associated Sturm series is:

\begin{array}{l} p_0(\lambda)=a_0 \lambda^2 -a_2 \\ p_1(\lambda)=a_1 \lambda \end{array}

The Sturm polynomials can be written as (here ):

p_i(\mu)= c_{i,0} \mu^{k-i} + c_{i,1} \mu^{k-i-2} + c_{i,2} \mu^{k-i-4}+\cdots

The above proposition 2 tells that one must have:

c_{0,0} = 1 >0, c_{1,0}=- \mu = 0, c_{0,1}=-1 <0.

Because 1 > 0 and −1 < 0 are obvious, one can conclude that a Hopf bifurcation may occur for Van der Pol oscillator if .

Read more about this topic:  Hopf Bifurcation

Famous quotes containing the word example:

    “Our intellect is not the most subtle, the most powerful, the most appropriate, instrument for revealing the truth. It is life that, little by little, example by example, permits us to see that what is most important to our heart, or to our mind, is learned not by reasoning but through other agencies. Then it is that the intellect, observing their superiority, abdicates its control to them upon reasoned grounds and agrees to become their collaborator and lackey.”
    —Marcel Proust (1871–1922)