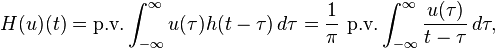Hilbert Transform - Introduction

Introduction

The Hilbert transform of u can be thought of as the convolution of u(t) with the function h(t) = 1/(π t). Because h(t) is not integrable the integrals defining the convolution do not converge. Instead, the Hilbert transform is defined using the Cauchy principal value (denoted here by p.v.) Explicitly, the Hilbert transform of a function (or signal) u(t) is given by

H(u)(t) = \text{p.v.} \int_{-\infty}^{\infty}u(\tau) h(t-\tau)\, d\tau =\frac{1}{\pi} \ \text{p.v.} \int_{-\infty}^{\infty} \frac{u(\tau)}{t-\tau}\, d\tau,

provided this integral exists as a principal value. This is precisely the convolution of u with the tempered distribution p.v. 1/πt (due to Schwartz (1950); see Pandey (1996, Chapter 3)). Alternatively, by changing variables, the principal value integral can be written explicitly (Zygmund 1968, §XVI.1) as

When the Hilbert transform is applied twice in succession to a function u, the result is negative u:

provided the integrals defining both iterations converge in a suitable sense. In particular, the inverse transform is −H. This fact can most easily be seen by considering the effect of the Hilbert transform on the Fourier transform of (see Relationship with the Fourier transform, below).

For an analytic function in upper half-plane the Hilbert transform describes the relationship between the real part and the imaginary part of the boundary values. That is, if f(z) is analytic in the plane Im z > 0 and u(t) = Re f(t + 0·i ) then Im f(t + 0·i ) = H(u)(t) up to an additive constant, provided this Hilbert transform exists.

Read more about this topic:  Hilbert Transform

Famous quotes containing the word introduction:

    “We used chamber-pots a good deal.... My mother ... loved to repeat: “When did the queen reign over China?” This whimsical and harmless scatological pun was my first introduction to the wonderful world of verbal transformations, and also a first perception that a joke need not be funny to give pleasure.”
    —Angela Carter (1940–1992)

    “Such is oftenest the young man’s introduction to the forest, and the most original part of himself. He goes thither at first as a hunter and fisher, until at last, if he has the seeds of a better life in him, he distinguishes his proper objects, as a poet or naturalist it may be, and leaves the gun and fish-pole behind. The mass of men are still and always young in this respect.”
    —Henry David Thoreau (1817–1862)

    “My objection to Liberalism is this—that it is the introduction into the practical business of life of the highest kind—namely, politics—of philosophical ideas instead of political principles.”
    —Benjamin Disraeli (1804–1881)