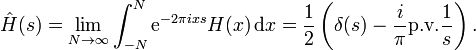Heaviside Step Function - Fourier Transform

Fourier Transform

The Fourier transform of the Heaviside step function is a distribution. Using one choice of constants for the definition of the Fourier transform we have

\hat{H}(s) = \lim_{N\to\infty}\int^N_{-N} \mathrm{e}^{-2\pi i x s} H(x)\,{\rm d}x = \frac{1}{2} \left( \delta(s) - \frac{i}{\pi}\text{p.v.}\frac{1}{s} \right).

Here is the distribution that takes a test function to the Cauchy principal value of The limit appearing in the integral is also taken in the sense of (tempered) distributions.

Read more about this topic:  Heaviside Step Function

Famous quotes containing the word transform:

    “But I must needs take my petulance, contrasting it with my accustomed morning hopefulness, as a sign of the ageing of appetite, of a decay in the very capacity of enjoyment. We need some imaginative stimulus, some not impossible ideal which may shape vague hope, and transform it into effective desire, to carry us year after year, without disgust, through the routine- work which is so large a part of life.”
    —Walter Pater (1839–1894)