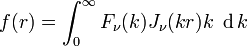Hankel Transform

In mathematics, the Hankel transform expresses any given function f(r) as the weighted sum of an infinite number of Bessel functions of the first kind Jν(kr). The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r-axis. The necessary coefficient Fν of each Bessel function in the sum, as a function of the scaling factor k constitutes the transformed function.

More precisely, the Hankel transform of order ν of a function f(r) is given by:

F_\nu(k) = \int_0^\infty f(r)J_\nu(kr)\,r\,\operatorname{d}r

where Jν is the Bessel function of the first kind of order ν with ν ≥ −1/2. The inverse Hankel transform of Fν(k) is defined as:

f(r) =\int_0^\infty F_\nu(k)J_\nu(kr) k~\operatorname{d}k

which can be readily verified using the orthogonality relationship described below. The Hankel transform is an integral transform and was first developed by the mathematician Hermann Hankel. It is also known as the Fourier–Bessel transform. Just as the Fourier transform for an infinite interval is related to the Fourier series over a finite interval, so the Hankel transform over an infinite interval is related to the Fourier–Bessel series over a finite interval.

Read more about Hankel Transform:  Domain of Definition, Orthogonality, The Plancherel Theorem and Parseval's Theorem, Some Hankel Transform Pairs

Famous quotes containing the word transform:

    “He had said that everything possessed
    The power to transform itself, or else,
    And what meant more, to be transformed.”
    —Wallace Stevens (1879–1955)