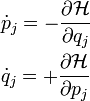Simplified Overview of Uses
The value of the Hamiltonian is the total energy of the system being described. For a closed system, it is the sum of the kinetic and potential energy in the system. There is a set of differential equations known as the Hamilton equations which give the time evolution of the system. Hamiltonians can be used to describe such simple systems as a bouncing ball, a pendulum or an oscillating spring in which energy changes from kinetic to potential and back again over time. Hamiltonians can also be employed to model the energy of other more complex dynamic systems such as planetary orbits in celestial mechanics and also in quantum mechanics.
The Hamilton equations are generally written as follows:
where the dot denotes the ordinary derivative with respect to time of generalized momenta pj = pj(t) and the generalized coordinates qj = qj(t), where j = 1,2...n.
More explicitly, one can equivalently write
where the functions q and p take values in a vector space, and function is the (scalar valued) Hamiltonian function, and specify the domain of values in which the parameter t (time) varies.
Hamilton's equations are symmetric in the generalized coordinates and momenta, meaning the interchange and hence leaves the equations unchanged. Naturally, the more degrees of freedom the system has, the more complicated its behavior (predicted by the solutions), since the degrees of freedom correspond to the configuration of the system i.e. (generalized) positions, momenta and the rates at which these change (time derivatives). As such, for more than two massive particles the solutions cannot be found exactly - the many-body problem. It is still possible to obtain qualitative knowledge about the system by approximate analysis of the differential equations.
For a detailed derivation of these equations from Lagrangian mechanics, see below.
Read more about this topic: Hamiltonian Mechanics
Famous quotes containing the word simplified:
“I have simplified my politics into an utter detestation of all existing governments; and, as it is the shortest and most agreeable and summary feeling imaginable, the first moment of an universal republic would convert me into an advocate for single and uncontradicted despotism. The fact is, riches are power, and poverty is slavery all over the earth, and one sort of establishment is no better, nor worse, for a people than another.”
—George Gordon Noel Byron (1788–1824)