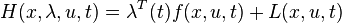Hamiltonian (control Theory) - Definition of The Hamiltonian

Definition of The Hamiltonian

H(x,\lambda,u,t)=\lambda^T(t)f(x,u,t)+L(x,u,t) \,

where is a vector of costate variables of the same dimension as the state variables .

For information on the properties of the Hamiltonian, see Pontryagin's minimum principle.

Read more about this topic:  Hamiltonian (control Theory)

Famous quotes containing the words definition of and/or definition:

    “It’s a rare parent who can see his or her child clearly and objectively. At a school board meeting I attended . . . the only definition of a gifted child on which everyone in the audience could agree was “mine.””
    —Jane Adams (20th century)

    “The definition of good prose is proper words in their proper places; of good verse, the most proper words in their proper places. The propriety is in either case relative. The words in prose ought to express the intended meaning, and no more; if they attract attention to themselves, it is, in general, a fault.”
    —Samuel Taylor Coleridge (1772–1834)