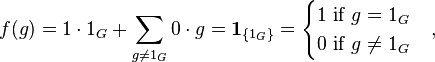Group Ring - Some Basic Properties

Some Basic Properties

Assuming that the ring R has a unit element 1, and denoting the group unit by 1G, the ring R contains a subring isomorphic to R, and its group of invertible elements contains a subgroup isomorphic to G. For considering the indicator function of {1G}, which is the vector f defined by

f(g)= 1\cdot 1_G + \sum_{g\not= 1_G}0 \cdot g= \mathbf{1}_{\{1_G\}}=\begin{cases} 1\text{ if }g = 1_G \\ 0\text{ if }g \ne 1_G \end{cases},

the set of all scalar multiples of f is a subring of R isomorphic to R. And if we map each element s of G to the indicator function of {s}, which is the vector f defined by

f(g)= 1\cdot s + \sum_{g\not= s}0 \cdot g= \mathbf{1}_{\{s\}}=\begin{cases} 1\text{ if }g = s \\ 0\text{ if }g \ne s \end{cases}

the resulting mapping is an injective group homomorphism (with respect to multiplication, not addition, in R).

If R and G are both commutative (i.e., R is commutative and G is an abelian group), R is commutative.

If H is a subgroup of G, then R is a subring of R. Similarly, if S is a subring of R, S is a subring of R.

Read more about this topic:  Group Ring

Famous quotes containing the words basic and/or properties:

    “A kiss can be a comma, a question mark or an exclamation point. That’s basic spelling that every woman ought to know.”
    —Mistinguett (1874–1956)

    “A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
    —Ralph Waldo Emerson (1803–1882)