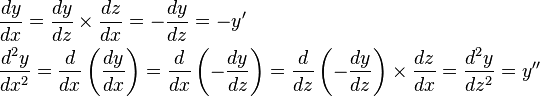Frobenius Solution To The Hypergeometric Equation - Solution Around x = 1

Solution Around x = 1

Let us now study the singular point x = 1. To see if it is regular,

\begin{align} &\lim_{x \to a} \frac{(x - a) P_1(x)}{P_2(x)} = \lim_{x \to 1} \frac{(x - 1) (\gamma - (1 + \alpha + \beta)x)}{x(1 - x)} \\ &\quad = \lim_{x \to 1} \frac{-(\gamma - (1 + \alpha + \beta)x)}{x} = 1 + \alpha + \beta - \gamma \\ &\lim_{x \to a} \frac{(x - a)^2 P_0(x)}{P_2(x)} = \lim_{x \to 1} \frac{(x - 1)^2 (-\alpha\beta)}{x(1 - x)} = \lim_{x \to 1} \frac{(x - 1) \alpha \beta}{x} = 0 \end{align}

Hence, both limits exist and x = 1 is a regular singular point. Now, instead of assuming a solution on the form

we will try to express the solutions of this case in terms of the solutions for the point x = 0. We proceed as follows: we had the hypergeometric equation

Let z = 1 - x. Then

\begin{align} &\frac{dy}{dx} = \frac{dy}{dz} \times \frac{dz}{dx} = -\frac{dy}{dz} = -y' \\ &\frac{d^2 y}{dx^2} = \frac{d}{dx}\left( \frac{dy}{dx} \right) = \frac{d}{dx}\left( -\frac{dy}{dz} \right) = \frac{d}{dz}\left( -\frac{dy}{dz} \right) \times \frac{dz}{dx} =\frac{d^{2}y}{dz^{2}} = y'' \end{align}

Hence, the equation takes the form

Since z = 1 - x, the solution of the hypergeometric equation at x = 1 is the same as the solution for this equation at z = 0. But the solution at z = 0 is identical to the solution we obtained for the point x = 0, if we replace each γ by α + β - γ + 1. Hence, to get the solutions, we just make this substitution in the previous results. Note also that for x = 0, c1 = 0 and c2 = 1 - γ. Hence, in our case, c1 = 0 while c2 = γ - α - β. Let us now write the solutions. In the following we replaced each z by 1 - x.

Read more about this topic:  Frobenius Solution To The Hypergeometric Equation

Famous quotes containing the word solution:

    “The Settlement ... is an experimental effort to aid in the solution of the social and industrial problems which are engendered by the modern conditions of life in a great city. It insists that these problems are not confined to any one portion of the city. It is an attempt to relieve, at the same time, the overaccumulation at one end of society and the destitution at the other ...”
    —Jane Addams (1860–1935)