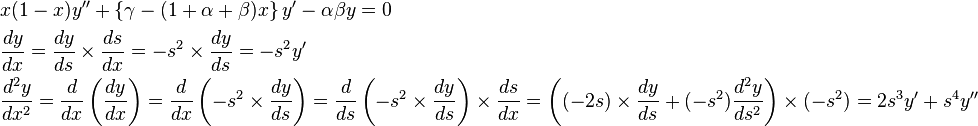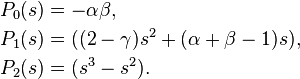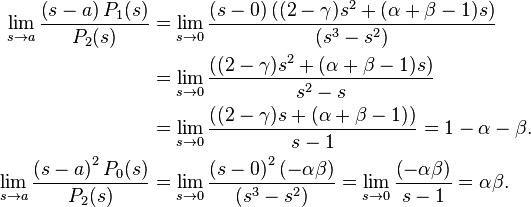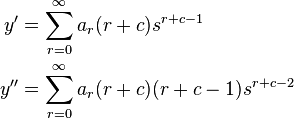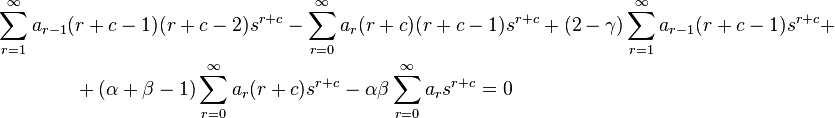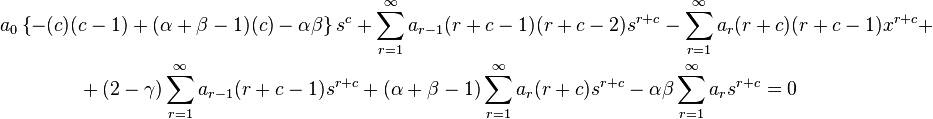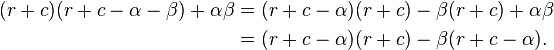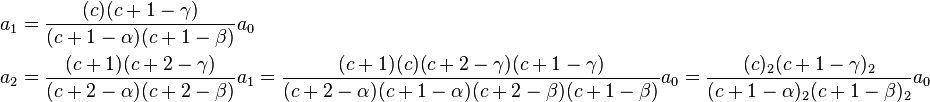Frobenius Solution To The Hypergeometric Equation - Solution Around Infinity

Solution Around Infinity

Finally, we study the singularity as x → ∞. Since we can't study this directly, we let x = s−1. Then the solution of the equation as x → ∞ is identical to the solution of the modified equation when s = 0. We had

\begin{align} & x(1-x)y''+\left\{ \gamma -(1+\alpha +\beta )x \right\}y'-\alpha \beta y=0 \\ & \frac{dy}{dx}=\frac{dy}{ds}\times \frac{ds}{dx}=-s^2\times \frac{dy}{ds}=-s^2y' \\ & \frac{d^{2}y}{dx^{2}}=\frac{d}{dx}\left( \frac{dy}{dx} \right)=\frac{d}{dx}\left( -s^2 \times \frac{dy}{ds} \right)=\frac{d}{ds}\left( -s^2 \times \frac{dy}{ds} \right)\times \frac{ds}{dx} = \left( (-2s)\times \frac{dy}{ds}+(-s^{2})\frac{d^{2}y}{ds^{2}} \right) \times (-s^{2})=2s^{3}y'+s^{4}y'' \end{align}

Hence, the equation takes the new form

which reduces to

Let

\begin{align} P_{0}(s) &=-\alpha \beta, \\ P_{1}(s) &=((2-\gamma )s^{2}+(\alpha +\beta -1)s), \\ P_{2}(s) &=(s^{3}-s^{2}). \end{align}

As we said, we shall only study the solution when s = 0. As we can see, this is a singular point since P2(0) = 0. To see if it's regular,

\begin{align} \lim_{s \to a} \frac{\left( s-a \right)P_{1}(s)}{P_{2}(s)} & =\lim_{s \to 0} \frac{\left( s-0 \right)((2-\gamma )s^{2}+(\alpha +\beta -1)s)}{(s^{3}-s^{2})} \\ &= \lim_{s \to 0} \frac{((2-\gamma )s^{2}+(\alpha +\beta -1)s)}{s^{2}-s} \\ & =\lim_{s \to 0} \frac{((2-\gamma )s+(\alpha +\beta -1))}{s-1}=1-\alpha -\beta. \\ \lim_{s \to a} \frac{\left( s-a \right)^{2}P_{0}(s)}{P_{2}(s)} &=\lim_{s \to 0} \frac{\left( s-0 \right)^{2}\left( -\alpha \beta \right)}{(s^{3}-s^{2})}=\lim_{s \to 0} \frac{\left( -\alpha \beta \right)}{s-1}=\alpha \beta. \end{align}

Hence, both limits exist and s = 0 is a regular singular point. Therefore, we assume the solution takes the form

with a0 ≠ 0.

Hence,

\begin{align} y'&=\sum\limits_{r=0}^{\infty }{a_{r}(r+c)s^{r+c-1}}\\ y''&=\sum\limits_{r=0}^{\infty }{a_{r}(r+c)(r+c-1)s^{r+c-2}} \end{align}

Substituting in the modified hypergeometric equation we get

And therefore:

i.e.,

In order to simplify this equation, we need all powers to be the same, equal to r + c, the smallest power. Hence, we switch the indices as follows

\begin{align} & \sum_{r=1}^{\infty }{a_{r-1}(r+c-1)(r+c-2)s^{r+c}}-\sum_{r=0}^{\infty }{a_{r}(r+c)(r+c-1)s^{r+c}} +(2-\gamma )\sum_{r=1}^{\infty }{a_{r-1}(r+c-1)s^{r+c}}+ \\ & \qquad \qquad + (\alpha +\beta -1)\sum_{r=0}^{\infty }{a_{r}(r+c)s^{r+c}}-\alpha \beta \sum_{r=0}^{\infty }{a_{r}s^{r+c}}=0 \end{align}

Thus, isolating the first term of the sums starting from 0 we get

\begin{align} & a_{0}\left\{ -(c)(c-1)+(\alpha +\beta -1)(c)-\alpha \beta \right\}s^{c}+\sum_{r=1}^{\infty }{a_{r-1}(r+c-1)(r+c-2)s^{r+c}} -\sum_{r=1}^{\infty }{a_{r}(r+c)(r+c-1)x^{r+c}}+\\ & \qquad \qquad + (2-\gamma )\sum_{r=1}^{\infty }{a_{r-1}(r+c-1)s^{r+c}} +(\alpha +\beta -1)\sum_{r=1}^{\infty }{a_{r}(r+c)s^{r+c}}-\alpha \beta \sum_{r=1}^{\infty }{a_{r}s^{r+c}}=0 \end{align}

Now, from the linear independence of all powers of s (i.e., of the functions 1, s, s2, ...), the coefficients of sk vanish for all k. Hence, from the first term we have

which is the indicial equation. Since a0 ≠ 0, we have

Hence, c1 = α and c2 = β.

Also, from the rest of the terms we have

Hence,

But

\begin{align} (r+c)(r+c-\alpha -\beta )+\alpha \beta &=(r+c-\alpha )(r+c)-\beta (r+c)+\alpha \beta \\ & =(r+c-\alpha )(r+c)-\beta (r+c-\alpha ). \end{align}

Hence, we get the recurrence relation

Let's now simplify this relation by giving ar in terms of a0 instead of ar−1. From the recurrence relation,

\begin{align} a_1 &=\frac{(c)(c+1-\gamma )}{(c+1-\alpha )(c+1-\beta )}a_{0} \\ a_2 &=\frac{(c+1)(c+2-\gamma )}{(c+2-\alpha )(c+2-\beta )}a_{1}=\frac{(c+1)(c)(c+2-\gamma )(c+1-\gamma )}{(c+2-\alpha )(c+1-\alpha )(c+2-\beta )(c+1-\beta )}a_{0} = \frac{(c)_{2}(c+1-\gamma )_{2}}{(c+1-\alpha )_{2}(c+1-\beta )_{2}}a_{0} \end{align}

As we can see,

Hence, our assumed solution takes the form

We are now ready to study the solutions corresponding to the different cases for c1 − c2 = α − β.

Read more about this topic:  Frobenius Solution To The Hypergeometric Equation

Famous quotes containing the words solution and/or infinity:

    “There is a lot of talk now about metal detectors and gun control. Both are good things. But they are no more a solution than forks and spoons are a solution to world hunger.”
    —Anna Quindlen (b. 1953)

    “The poetic notion of infinity is far greater than that which is sponsored by any creed.”
    —Joseph Brodsky (b. 1940)