Forces Acting On A Half-plane
For the special case where, the wedge is converted into a half-plane with a normal force and a tangential force. In that case
Therefore the stresses are
and the displacements are (using Michell's solution)
The dependence of the displacements implies that the displacement grows the further one moves from the point of application of the force (and is unbounded at infinity). This feature of the Flamant solution is confusing and appears unphysical. For a discussion of the issue see http://imechanica.org/node/319.
Read more about this topic: Flamant Solution
Famous quotes containing the words forces and/or acting:
“When we are in love, the sentiment is too great to be contained whole within us; it radiates out to our beloved, finds in her a surface which stops it, forces it to return to its point of departure, and it is this rebound of our own tenderness which we call the other’s affection and which charms us more than when it first went out because we do not see that it comes from us.”
—Marcel Proust (1871–1922)
“It especially helps if you know that we’re all faking our adulthood—even your parents and their parents. Beneath these adult trappings—in our president, in our parents, in you and me—lurk the emotions of a child. If we know that only about ourselves, we become infantile; if we understand that about everybody, then we have nothing to be ashamed of—unless, of course, we go around acting like a child and expecting everyone else to act like grownups.”
—Frank Pittman (20th century)

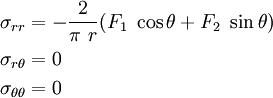
![\begin{align} u_r & = -\cfrac{1}{4\pi\mu}\left[F_1\{(\kappa-1)\theta\sin\theta - \cos\theta + (\kappa+1)\ln r\cos\theta\} + \right. \\ & \qquad \qquad \left. F_2\{(\kappa-1)\theta\cos\theta + \sin\theta - (\kappa+1)\ln r\sin\theta\}\right]\\ u_\theta & = -\cfrac{1}{4\pi\mu}\left[F_1\{(\kappa-1)\theta\cos\theta - \sin\theta - (\kappa+1)\ln r\sin\theta\} - \right. \\ & \qquad \qquad \left. F_2\{(\kappa-1)\theta\sin\theta + \cos\theta + (\kappa+1)\ln r\cos\theta\}\right] \end{align}](http://upload.wikimedia.org/math/4/9/6/496b6f7767598c7f1ed4d634ef2210bb.png)