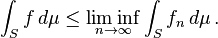Fatou's Lemma - Standard Statement of Fatou's Lemma

Standard Statement of Fatou's Lemma

Let f1, f2, f3, . . . be a sequence of non-negative measurable functions on a measure space (S,Σ,μ). Define the function f : S → a.e. pointwise limit by

f(s) =\liminf_{n\to\infty} f_n(s),\qquad s\in S.

Then f  is measurable and

\int_S f\,d\mu \le \liminf_{n\to\infty} \int_S f_n\,d\mu\,.

Note: The functions are allowed to attain the value +∞ and the integrals may also be infinite.

Read more about this topic:  Fatou's Lemma

Famous quotes containing the words standard and/or statement:

    “A disposition to preserve, and an ability to improve, taken together, would be my standard of a statesman.”
    —Edmund Burke (1729–1797)

    “The force of truth that a statement imparts, then, its prominence among the hordes of recorded observations that I may optionally apply to my own life, depends, in addition to the sense that it is argumentatively defensible, on the sense that someone like me, and someone I like, whose voice is audible and who is at least notionally in the same room with me, does or can possibly hold it to be compellingly true.”
    —Nicholson Baker (b. 1957)