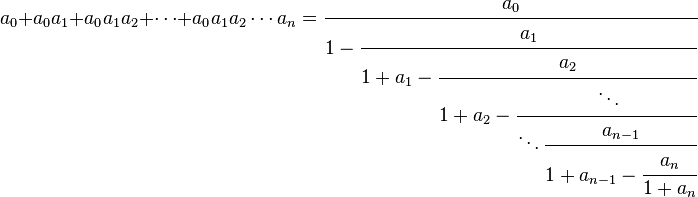The Original Formula
Euler derived the formula as an identity connecting a finite sum of products with a finite continued fraction.
The identity is easily established by induction on n, and is therefore applicable in the limit: if the expression on the left is extended to represent a convergent infinite series, the expression on the right can also be extended to represent a convergent infinite continued fraction.
Read more about this topic: Euler's Continued Fraction Formula
Famous quotes containing the words original and/or formula:
“The inspired scribbler always has the gift for gossip in our common usage ... he or she can always inspire the commonplace with an uncommon flavor, and transform trivialities by some original grace or sympathy or humor or affection.”
—Elizabeth Drew (1887–1965)
“In the most desirable conditions, the child learns to manage anxiety by being exposed to just the right amounts of it, not much more and not much less. This optimal amount of anxiety varies with the child’s age and temperament. It may also vary with cultural values.... There is no mathematical formula for calculating exact amounts of optimal anxiety. This is why child rearing is an art and not a science.”
—Alicia F. Lieberman (20th century)