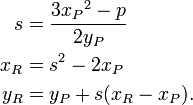Elliptic Curve - The Group Law

The Group Law

By adding a "point at infinity", we obtain the projective version of this curve. If P and Q are two points on the curve, then we can uniquely describe a third point which is the intersection of the curve with the line through P and Q. If the line is tangent to the curve at a point, then that point is counted twice; and if the line is parallel to the y-axis, we define the third point as the point "at infinity". Exactly one of these conditions then holds for any pair of points on an elliptic curve.

It is then possible to introduce a group operation, +, on the curve with the following properties: we consider the point at infinity to be 0, the identity of the group; and if a straight line intersects the curve at the points P, Q and R, then we require that P + Q + R = 0 in the group. One can check that this turns the curve into an abelian group, and thus into an abelian variety. It can be shown that the set of K-rational points (including the point at infinity) forms a subgroup of this group. If the curve is denoted by E, then this subgroup is often written as E(K).

The above group can be described algebraically as well as geometrically. Given the curve y2 = x3 − px − q over the field K (whose characteristic we assume to be neither 2 nor 3), and points P = (xP, yP) and Q = (xQ, yQ) on the curve, assume first that xP ≠ xQ. Let s be the slope of the line containing P and Q; i.e., s = (yP − yQ)⁄(xP − xQ). Since K is a field, s is well-defined. Then we can define R = P + Q = (xR, −yR) by

\begin{align} x_R &= s^2 - x_P - x_Q\\ y_R &= y_P + s(x_R - x_P). \end{align}

If xP = xQ, then there are two options: if yP = −yQ, including the case where yP = yQ = 0, then the sum is defined as 0; thus, the inverse of each point on the curve is found by reflecting it across the x-axis. If yP = yQ ≠ 0, then R = P + P = 2P = (xR, −yR) is given by

\begin{align} s &= \frac{3{x_P}^2 - p}{2y_P}\\ x_R &= s^2 - 2x_P\\ y_R &= y_P + s(x_R - x_P). \end{align}

Read more about this topic:  Elliptic Curve

Famous quotes containing the words group and/or law:

    “Even in harmonious families there is this double life: the group life, which is the one we can observe in our neighbour’s household, and, underneath, another—secret and passionate and intense—which is the real life that stamps the faces and gives character to the voices of our friends. Always in his mind each member of these social units is escaping, running away, trying to break the net which circumstances and his own affections have woven about him.”
    —Willa Cather (1873–1947)

    “Since you were so thankfully confused
    By law with someone else, you cannot be
    Semantically the same as that young beauty:
    It was of her that these two words were used.”
    —Philip Larkin (1922–1986)