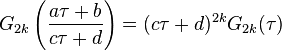Eisenstein Series - Eisenstein Series For The Modular Group

Eisenstein Series For The Modular Group

Let be a complex number with strictly positive imaginary part. Define the holomorphic Eisenstein series of weight where is an integer, by the following series:

G_{2k}(\tau) = \sum_{ (m,n)\in\mathbb{Z}^2\backslash(0,0)} \frac{1}{(m+n\tau )^{2k}}.

This series absolutely converges to a holomorphic function of in the upper half-plane and its Fourier expansion given below shows that it extends to a holomorphic function at It is a remarkable fact that the Eisenstein series is a modular form. Indeed, the key property is its invariance. Explicitly if and then

G_{2k} \left( \frac{ a\tau +b}{ c\tau + d} \right) = (c\tau +d)^{2k} G_{2k}(\tau)

and is therefore a modular form of weight . Note that it is important to assume that otherwise it would be illegitimate to change the order of summation, and the -invariance would not hold. In fact, there are no nontrivial modular forms of weight 2. Nevertheless, an analogue of the holomorphic Eisenstein series can be defined even for although it would only be a quasimodular form.

Read more about this topic:  Eisenstein Series

Famous quotes containing the words series and/or group:

    “Through a series of gradual power losses, the modern parent is in danger of losing sight of her own child, as well as her own vision and style. It’s a very big price to pay emotionally. Too bad it’s often accompanied by an equally huge price financially.”
    —Sonia Taitz (20th century)

    “We begin with friendships, and all our youth is a reconnoitering and recruiting of the holy fraternity they shall combine for the salvation of men. But so the remoter stars seem a nebula of united light, yet there is no group which a telescope will not resolve; and the dearest friends are separated by impassable gulfs.”
    —Ralph Waldo Emerson (1803–1882)