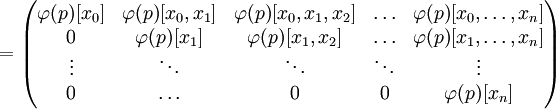Divided Differences - Polynomials and Power Series

Polynomials and Power Series

Divided differences of polynomials are particularly interesting, because they can benefit from the Leibniz rule. The matrix with

$J= \begin{pmatrix} x_0 & 1 & 0 & 0 & \cdots & 0 \\ 0 & x_1 & 1 & 0 & \cdots & 0 \\ 0 & 0 & x_2 & 1 & & 0 \\ \vdots & \vdots & & \ddots & \ddots & \\ 0 & 0 & 0 & 0 & & x_n \end{pmatrix}$

contains the divided difference scheme for the identity function with respect to the nodes, thus contains the divided differences for the power function with exponent . Consequently you can obtain the divided differences for a polynomial function with respect to the polynomial by applying (more precisely: its corresponding matrix polynomial function ) to the matrix .

$= \begin{pmatrix} \varphi(p) & \varphi(p) & \varphi(p) & \ldots & \varphi(p) \\ 0 & \varphi(p) & \varphi(p) & \ldots & \varphi(p) \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \ldots & 0 & 0 & \varphi(p) \end{pmatrix}$

This is known as Opitz' formula.

Now consider increasing the degree of to infinity, i.e. turn the Taylor polynomial to a Taylor series. Let be a function which corresponds to a power series. You can compute a divided difference scheme by computing the according matrix series applied to . If the nodes are all equal, then is a Jordan block and computation boils down to generalizing a scalar function to a matrix function using Jordan decomposition.

Read more about this topic: Divided Differences

Famous quotes containing the words power and/or series:

“The miracles of the church seem to me to rest not so much upon faces or voices or healing power coming suddenly near to us from afar off, but upon our perceptions being made finer, so that for a moment our eyes can see and our ears can hear what is there about us always.”
—Willa Cather (1873–1947)

“Personality is an unbroken series of successful gestures.”
—F. Scott Fitzgerald (1896–1940)