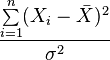Degrees of Freedom Parameters in Probability Distributions
Several commonly encountered statistical distributions (Student's t, Chi-Squared, F) have parameters that are commonly referred to as degrees of freedom. This terminology simply reflects that in many applications where these distributions occur, the parameter corresponds to the degrees of freedom of an underlying random vector, as in the preceding ANOVA example. Another simple example is: if are independent normal random variables, the statistic
follows a chi-squared distribution with n−1 degrees of freedom. Here, the degrees of freedom arises from the residual sum-of-squares in the numerator, and in turn the n−1 degrees of freedom of the underlying residual vector .
In the application of these distributions to linear models, the degrees of freedom parameters can take only integer values. The underlying families of distributions allow fractional values for the degrees-of-freedom parameters, which can arise in more sophisticated uses. One set of examples is problems where chi-squared approximations based on effective degrees of freedom are used. In other applications, such as modelling heavy-tailed data, a t or F distribution may be used as an empirical model. In these cases, there is no particular degrees of freedom interpretation to the distribution parameters, even though the terminology may continue to be used.
Read more about this topic: Degrees Of Freedom (statistics)
Famous quotes containing the words degrees of, degrees, freedom, parameters and/or probability:
“So that the life of a writer, whatever he might fancy to the contrary, was not so much a state of composition, as a state of warfare; and his probation in it, precisely that of any other man militant upon earth,—both depending alike, not half so much upon the degrees of his WIT—as his RESISTANCE.”
—Laurence Sterne (1713–1768)
“For the profit of travel: in the first place, you get rid of a few prejudices.... The prejudiced against color finds several hundred millions of people of all shades of color, and all degrees of intellect, rank, and social worth, generals, judges, priests, and kings, and learns to give up his foolish prejudice.”
—Herman Melville (1819–1891)
“[T]here is a Wit for Discourse, and a Wit for Writing. The Easiness and Familiarity of the first, is not to savour in the least of Study; but the Exactness of the other, is to admit of something like the Freedom of Discourse, especially in Treatises of Humanity, and what regards the Belles Lettres.”
—Richard Steele (1672–1729)
“What our children have to fear is not the cars on the highways of tomorrow but our own pleasure in calculating the most elegant parameters of their deaths.”
—J.G. (James Graham)
“The probability of learning something unusual from a newspaper is far greater than that of experiencing it; in other words, it is in the realm of the abstract that the more important things happen in these times, and it is the unimportant that happens in real life.”
—Robert Musil (1880–1942)