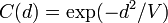Parametric Families of Covariance Functions
A simple stationary parametric covariance function is the "exponential covariance function"
where V is a scaling parameter, and d=d(x,y) is the distance between two points. Sample paths of a Gaussian process with the exponential covariance function are not smooth. The "squared exponential covariance function"
is a stationary covariance function with smooth sample paths.
The Matérn covariance function and rational quadratic covariance function are two parametric families of stationary covariance functions. The Matérn family includes the exponential and squared exponential covariance functions as special cases.
Read more about this topic: Covariance Function
Famous quotes containing the words families and/or functions:
“The ideal of the self-sufficient American family is a myth, dangerous because most families, especially affluent families, do in fact make use of a range of services to survive. Families needing one or another kind of help are not morally deficient; most families do need assistance at one time or another.”
—Joseph Featherstone (20th century)
“The mind is a finer body, and resumes its functions of feeding, digesting, absorbing, excluding, and generating, in a new and ethereal element. Here, in the brain, is all the process of alimentation repeated, in the acquiring, comparing, digesting, and assimilating of experience. Here again is the mystery of generation repeated.”
—Ralph Waldo Emerson (1803–1882)