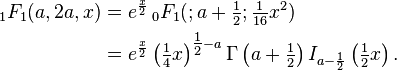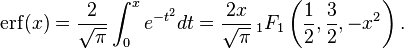Confluent Hypergeometric Function - Special Cases

Special Cases

Functions that can be expressed as special cases of the confluent hypergeometric function include:

  • Bateman's function
  • Bessel functions and many related functions such as Airy functions, Kelvin functions, Hankel functions.

For example, the special case the function reduces to a Bessel function:

\begin{align}\, _1F_1(a,2a,x)&= e^{\frac x 2}\, _0F_1 (a+\tfrac{1}{2}; \tfrac{1}{16}x^2) \\ &= e^{\frac x 2} \left(\tfrac{1}{4}x\right)^{\tfrac{1}{2}-a} \Gamma\left(a+\tfrac{1}{2}\right) I_{a-\frac 1 2}\left(\tfrac{1}{2}x\right).\end{align}

This identity is sometimes also referred to as Kummer's second transformation. Similarly

where is related to Bessel polynomial for integer .

  • The error function can be expressed as
\mathrm{erf}(x)= \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2} dt= \frac{2x}{\sqrt{\pi}}\,_1F_1\left(\frac{1}{2},\frac{3}{2},-x^2\right).
  • Coulomb wave function
  • Cunningham functions
  • Elementary functions such as sin, cos, exp. For example,
  • Exponential integral and related functions such as the sine integral, logarithmic integral
  • Hermite polynomials
  • Incomplete gamma function
  • Laguerre polynomials
  • Parabolic cylinder function (or Weber function)
  • Poisson–Charlier function
  • Toronto functions
  • Whittaker functions Mκ,μ(z), Wκ,μ(z) are solutions of Whittaker's equation that can be expressed in terms of Kummer functions M and U by
  • The general p-th raw moment (p not necessarily an integer) can be expressed as
(the function's second branch cut can be chosen by multiplying with ).

Read more about this topic:  Confluent Hypergeometric Function

Famous quotes containing the words special and/or cases:

    “The universal social pressure upon women to be all alike, and do all the same things, and to be content with identical restrictions, has resulted not only in terrible suffering in the lives of exceptional women, but also in the loss of unmeasured feminine values in special gifts. The Drama of the Woman of Genius has too often been a tragedy of misshapen and perverted power.”
    —Anna Garlin Spencer (1851–1931)

    “In the beautiful, man sets himself up as the standard of perfection; in select cases he worships himself in it.... Man believes that the world itself is filled with beauty—he forgets that it is he who has created it. He alone has bestowed beauty upon the world—alas! only a very human, an all too human, beauty.”
    —Friedrich Nietzsche (1844–1900)