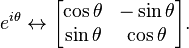Isomorphisms
The circle group shows up in a variety of forms in mathematics. We list some of the more common forms here. Specifically, we show that
Note that the slash (/) denotes here quotient group.
The set of all 1×1 unitary matrices clearly coincides with the circle group; the unitary condition is equivalent to the condition that its element have absolute value 1. Therefore, the circle group is canonically isomorphic to U(1), the first unitary group.
The exponential function gives rise to a group homomorphism exp : R → T from the additive real numbers R to the circle group T via the map
The last equality is Euler's formula. The real number θ corresponds to the angle on the unit circle as measured from the positive x-axis. That this map is a homomorphism follows from the fact that the multiplication of unit complex numbers corresponds to addition of angles:
This exponential map is clearly a surjective function from R to T. It is not, however, injective. The kernel of this map is the set of all integer multiples of 2π. By the first isomorphism theorem we then have that
After rescaling we can also say that T is isomorphic to R/Z.
If complex numbers are realized as 2×2 real matrices (see complex number), the unit complex numbers correspond to 2×2 orthogonal matrices with unit determinant. Specifically, we have
The circle group is therefore isomorphic to the special orthogonal group SO(2). This has the geometric interpretation that multiplication by a unit complex number is a proper rotation in the complex plane, and every such rotation is of this form.
Read more about this topic: Circle Group