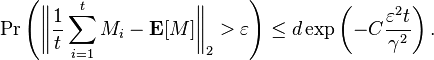Matrix Chernoff Bound
Rudolf Ahlswede and Andreas Winter introduced (Ahlswede & Winter 2003) a Chernoff bound for matrix-valued random variables.
If is distributed according to some distribution over matrices with zero mean, and if are independent copies of then for any ,
where holds almost surely and is an absolute constant.
Notice that the number of samples in the inequality depends logarithmically on . In general, unfortunately, such a dependency is inevitable: take for example a diagonal random sign matrix of dimension . The operator norm of the sum of independent samples is precisely the maximum deviation among independent random walks of length . In order to achieve a fixed bound on the maximum deviation with constant probability, it is easy to see that should grow logarithmically with in this scenario.
The following theorem can be obtained by assuming has low rank, in order to avoid the dependency on the dimensions.
Read more about this topic: Chernoff Bound
Famous quotes containing the words matrix and/or bound:
“As all historians know, the past is a great darkness, and filled with echoes. Voices may reach us from it; but what they say to us is imbued with the obscurity of the matrix out of which they come; and try as we may, we cannot always decipher them precisely in the clearer light of our day.”
—Margaret Atwood (b. 1939)
“We are all bound to the throne of the Supreme Being by a flexible chain which restrains without enslaving us. The most wonderful aspect of the universal scheme of things is the action of free beings under divine guidance.”
—Joseph De Maistre (1753–1821)