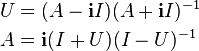Cayley Transform - Operator Map

Operator Map

An infinite-dimensional version of an inner product space is a Hilbert space, and we can no longer speak of matrices. However, matrices are merely representations of linear operators, and these we still have. So, generalizing both the matrix mapping and the complex plane mapping, we may define a Cayley transform of operators.

\begin{align} U &{}= (A - \bold{i}I) (A + \bold{i}I)^{-1} \\ A &{}= \bold{i}(I + U) (I - U)^{-1} \end{align}

Here the domain of U, dom U, is (A+iI) dom A. See self-adjoint operator for further details.

Read more about this topic:  Cayley Transform

Famous quotes containing the word map:

    “When I had mapped the pond ... I laid a rule on the map lengthwise, and then breadthwise, and found, to my surprise, that the line of greatest length intersected the line of greatest breadth exactly at the point of greatest depth.”
    —Henry David Thoreau (1817–1862)