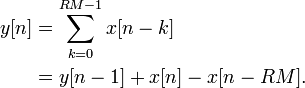CIC As A Moving Average Filter
A CIC filter is an efficient implementation of a moving average filter. To see this, consider how a moving average filter can be implemented recursively by adding the newest sample to the previous result and subtracting the oldest sample. Omitting the division by, we have:
The second equality corresponds to a comb followed by an integrator . The conventional CIC structure is obtained by cascading identical moving average filters, then rearranging the sections to place all integrators first (decimator) or combs first (interpolator). Such rearrangement is possible because both combs and integrators are LTI. For an interpolator, the upsampler which normally precedes the interpolation filter can be passed through the comb sections using a Noble identity, reducing the number of delay elements needed by a factor of . Similarly, for a decimator, the downsampler which normally follows the decimation filter can be moved before the comb sections.
The equivalence of a CIC to moving average filter allows us to trivially calculate its bit growth as .
Read more about this topic: Cascaded Integrator-comb Filter
Famous quotes containing the words moving and/or average:
“With varying vanities, from ev’ry part,
They shift the moving toyshop of their heart;”
—Alexander Pope (1688–1744)
“In the middle classes the gifted son of a family is always the poorest—usually a writer or artist with no sense for speculation—and in a family of peasants, where the average comfort is just over penury, the gifted son sinks also, and is soon a tramp on the roadside.”
—J.M. (John Millington)