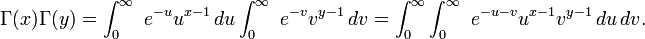Beta Function - Relationship Between Gamma Function and Beta Function

Relationship Between Gamma Function and Beta Function

To derive the integral representation of the beta function, write the product of two factorials as

\Gamma(x)\Gamma(y) = \int_0^\infty\ e^{-u} u^{x-1}\,du \int_0^\infty\ e^{-v} v^{y-1}\,dv =\int_0^\infty\int_0^\infty\ e^{-u-v} u^{x-1}v^{y-1}\,du \,dv. \!

Changing variables by putting u=zt, v=z(1-t) shows that this is

\int_{z=0}^\infty\int_{t=0}^1\ e^{-z} (zt)^{x-1}(z(1-t))^{y-1}z\,dt \,dz =\int_{z=0}^\infty \ e^{-z}z^{x+y-1} \,dz\int_{t=0}^1t^{x-1}(1-t)^{y-1}\,dt. \!

Hence

\Gamma(x)\,\Gamma(y)=\Gamma(x+y)\Beta(x,y) .

The stated identity may be seen as a particular case of the identity for the integral of a convolution. Taking

and, one has:
.

Read more about this topic:  Beta Function

Famous quotes containing the words relationship and/or function:

    “We must introduce a new balance in the relationship between the individual and the government—a balance that favors greater individual freedom and self-reliance.”
    —Gerald R. Ford (b. 1913)

    “The function of literature, through all its mutations, has been to make us aware of the particularity of selves, and the high authority of the self in its quarrel with its society and its culture. Literature is in that sense subversive.”
    —Lionel Trilling (1905–1975)