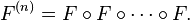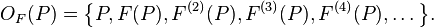Definitions and Notation From Discrete Dynamics
Let S be a set and let F : S → S be a map from S to itself. The iterate of F with itself n times is denoted
A point P ∈ S is periodic if F(n)(P) = P for some n > 1.
The point is preperiodic if F(k)(P) is periodic for some k ≥ 1.
The (forward) orbit of P is the set
Thus P is preperiodic if and only if its orbit OF(P) is finite.
Read more about this topic: Arithmetic Dynamics
Famous quotes containing the words definitions, discrete and/or dynamics:
“What I do not like about our definitions of genius is that there is in them nothing of the day of judgment, nothing of resounding through eternity and nothing of the footsteps of the Almighty.”
—G.C. (Georg Christoph)
“We have good reason to believe that memories of early childhood do not persist in consciousness because of the absence or fragmentary character of language covering this period. Words serve as fixatives for mental images. . . . Even at the end of the second year of life when word tags exist for a number of objects in the child’s life, these words are discrete and do not yet bind together the parts of an experience or organize them in a way that can produce a coherent memory.”
—Selma H. Fraiberg (20th century)
“Anytime we react to behavior in our children that we dislike in ourselves, we need to proceed with extreme caution. The dynamics of everyday family life also have a way of repeating themselves.”
—Cathy Rindner Tempelsman (20th century)