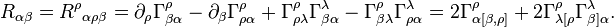Ricci Curvature - Definition

Definition

Suppose that is an n-dimensional Riemannian manifold, equipped with its Levi-Civita connection . The Riemannian curvature tensor of is the tensor defined by

on vector fields . Let denote the tangent space of M at a point p. For any pair of tangent vectors at p, the Ricci tensor evaluated at is defined to be the trace of the linear map given by

In local coordinates (using the Einstein summation convention), one has

where

In terms of the Riemann curvature tensor and the Christoffel symbols, one has

R_{\alpha\beta} = {R^\rho}_{\alpha\rho\beta} = \partial_{\rho}{\Gamma^\rho_{\beta\alpha}} - \partial_{\beta}\Gamma^\rho_{\rho\alpha} + \Gamma^\rho_{\rho\lambda} \Gamma^\lambda_{\beta\alpha} - \Gamma^\rho_{\beta\lambda}\Gamma^\lambda_{\rho\alpha} =2 \Gamma^{\rho}_{{\alpha}} + 2 \Gamma^\rho_{\lambda \alpha} .

Read more about this topic:  Ricci Curvature

Famous quotes containing the word definition:

    “According to our social pyramid, all men who feel displaced racially, culturally, and/or because of economic hardships will turn on those whom they feel they can order and humiliate, usually women, children, and animals—just as they have been ordered and humiliated by those privileged few who are in power. However, this definition does not explain why there are privileged men who behave this way toward women.”
    —Ana Castillo (b. 1953)

    “The man who knows governments most completely is he who troubles himself least about a definition which shall give their essence. Enjoying an intimate acquaintance with all their particularities in turn, he would naturally regard an abstract conception in which these were unified as a thing more misleading than enlightening.”
    —William James (1842–1910)

    “The definition of good prose is proper words in their proper places; of good verse, the most proper words in their proper places. The propriety is in either case relative. The words in prose ought to express the intended meaning, and no more; if they attract attention to themselves, it is, in general, a fault.”
    —Samuel Taylor Coleridge (1772–1834)