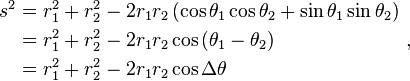Pythagorean Theorem - Consequences and Uses of The Theorem - Euclidean Distance in Various Coordinate Systems

Euclidean Distance in Various Coordinate Systems

The distance formula in Cartesian coordinates is derived from the Pythagorean theorem. If (x₁, y₁) and (x₂, y₂) are points in the plane, then the distance between them, also called the Euclidean distance, is given by

More generally, in Euclidean n-space, the Euclidean distance between two points, and, is defined, by generalization of the Pythagorean theorem, as:

If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or, in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras' theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates (r, θ) can be introduced as:

Then two points with locations (r₁, θ₁) and (r₂, θ₂) are separated by a distance s:

Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as:

using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the Generalized Pythagorean Theorem. From this result, for the case where the radii to the two locations are at right angles, the enclosed angle Δθ = π/2, and the form corresponding to Pythagoras' theorem is regained: The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles.