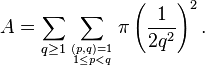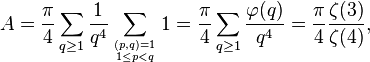Ford Circle - Total Area of Ford Circles

Total Area of Ford Circles

There is a link between the area of Ford circles, Euler's totient function φ, the Riemann zeta function ζ, and Apéry's constant ζ(3).

As no two Ford circles intersect, it follows immediately that the total area of the Ford circles

is less than 1. In fact the total area of these Ford circles is given by a convergent sum, which can be evaluated.

From the definition, the area is

A = \sum_{q\ge 1} \sum_{ (p, q)=1 \atop 1 \le p < q } \pi \left( \frac{1}{2 q^2} \right)^2.

Simplifying this expression gives

A = \frac{\pi}{4} \sum_{q\ge 1} \frac{1}{q^4} \sum_{ (p, q)=1 \atop 1 \le p < q } 1 = \frac{\pi}{4} \sum_{q\ge 1} \frac{\varphi(q)}{q^4} = \frac{\pi}{4} \frac{\zeta(3)}{\zeta(4)},

where the last equality reflects the Dirichlet generating function for Euler's totient function φ(q). Since ζ(4) = π 4/90, this finally becomes

Read more about this topic:  Ford Circle

Famous quotes containing the words total, area, ford and/or circles:

    “If you have only one smile in you, give it to the people you love. Don’t be surly at home, then go out in the street and start grinning “Good morning” at total strangers.”
    —Maya Angelou (b. 1928)

    “The area [of toilet training] is one where a child really does possess the power to defy. Strong pressure leads to a powerful struggle. The issue then is not toilet training but who holds the reins—mother or child? And the child has most of the ammunition!”
    —Dorothy Corkville Briggs (20th century)

    “Can a free people restrain crime without sacrificing fundamental liberties and a heritage of compassion?... Let us show that we can temper together those opposite elements of liberty and restraint into one consistent whole. Let us set an example for the world of a law-abiding America glorying in its freedom as well as its respect for law.”
    —Gerald R. Ford (b. 1913)

    “Before the birth of the New Woman the country was not an intellectual desert, as she is apt to suppose. There were teachers of the highest grade, and libraries, and countless circles in our towns and villages of scholarly, leisurely folk, who loved books, and music, and Nature, and lived much apart with them. The mad craze for money, which clutches at our souls to-day as la grippe does at our bodies, was hardly known then.”
    —Rebecca Harding Davis (1831–1910)