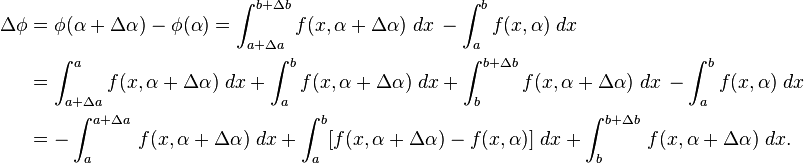Differentiation Under The Integral Sign - Derivation of The Principle of Differentiation Under The Integral Sign

Derivation of The Principle of Differentiation Under The Integral Sign

A definite integral is a function of its upper limit and its lower limit

If is a continuous function of or, then, from the definition of the definite integral,

and

since, from proof of the fundamental theorem of calculus,

\begin{align} \frac{\partial}{\partial b}\int_a^b f(x)\; dx &= \lim_{\Delta b \to 0} \frac{1}{\Delta b} \left \\ &= \lim_{\Delta b \to 0} \frac{1}{\Delta b} \int_b^{b+\Delta b} f(x)\,dx = \lim_{\Delta b \to 0} \frac{1}{\Delta b} \left \\ &= f(b) \qquad \text{and} \\ \frac{\partial}{\partial a}\int_a^b f(x)\; dx &= \lim_{\Delta a \to 0} \frac{1}{\Delta a} \left \\ &= \lim_{\Delta a \to 0} \frac{1}{\Delta a} \int_{a+\Delta a}^a f(x)\,dx = \lim_{\Delta a \to 0} \frac{1}{\Delta a} \left \\ &= -f(a). \end{align}

Suppose and are constant, and that involves a parameter which is constant in the integration but may vary to form different integrals. Then, by the definition of a function,

In general, this may be differentiated by differentiating under the integral sign; i.e.,

To prove this and, at the same time, to determine conditions under which the formula is true, we proceed as follows:

From

From the fact that we have

If is a continuous function of and when then for any there exists such that

for all values of

(This follows from the Heine–Cantor theorem that every continuous function on a compact set is uniformly continuous.)

Therefore, from and

we get and the fact that is, therefore, a continuous function.

Similarly if exists and is continuous, then for all there exists such that:

for all

Therefore,

\begin{align} \frac{\Delta \phi}{\Delta \alpha}&=\int_a^b\frac{f(x,\alpha+\Delta\alpha)-f(x,\alpha)}{\Delta \alpha}\;dx\\ &= \int_a^b \frac{\partial\,f(x,\alpha)}{\partial \alpha}\,dx + R\\ \text{where} \quad |R| &< \int_a^b \epsilon\; dx = \epsilon\;(b-a). \end{align}

Now, as, therefore,

This is the formula we set out to prove.

Now, suppose where and are functions of which take increments and respectively, when is increased by Then,

\begin{align} \Delta\phi &=\phi(\alpha+\Delta\alpha)-\phi(\alpha)=\int_{a+\Delta a}^{b+\Delta b}f(x,\alpha+\Delta\alpha)\;dx\,-\int_a^b f(x,\alpha)\;dx\, \\ &=\int_{a+\Delta a}^af(x,\alpha+\Delta\alpha)\;dx+\int_a^bf(x,\alpha+\Delta\alpha)\;dx+\int_b^{b+\Delta b}f(x,\alpha+\Delta\alpha)\;dx\,-\int_a^b f(x,\alpha)\;dx\, \\ &=-\int_a^{a+\Delta a}\,f(x,\alpha+\Delta\alpha)\;dx+\int_a^b\;dx+\int_b^{b+\Delta b}\,f(x,\alpha+\Delta\alpha)\;dx.\, \end{align}

A form of the mean value theorem, where can be applied to the first and last integrals of the formula for above, resulting in

Dividing by, letting noticing and and using the result yields

This is the general form of the Leibniz integral rule.

Read more about this topic:  Differentiation Under The Integral Sign

Famous quotes containing the words principle, integral and/or sign:

    “It were as wise to cast a violet into a crucible that you might discover the formal principle of its colour and odour, as seek to transfuse from one language into another the creations of a poet. The plant must spring again from its seed, or it will bear no flower—and this is the burthen of the curse of Babel.”
    —Percy Bysshe Shelley (1792–1822)

    “An island always pleases my imagination, even the smallest, as a small continent and integral portion of the globe. I have a fancy for building my hut on one. Even a bare, grassy isle, which I can see entirely over at a glance, has some undefined and mysterious charm for me.”
    —Henry David Thoreau (1817–1862)

    “No, no; but as in my idolatry
    I said to all my profane mistresses,
    Beauty, of pity, foulness only is
    A sign of rigour: so I say to thee,
    To wicked spirits are horrid shapes assign’d,
    This beauteous form assures a piteous mind.”
    —John Donne (1572–1631)