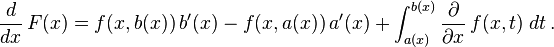Differentiation Under The Integral Sign

Differentiation under the integral sign is a useful operation in calculus. Suppose that it is required to differentiate with respect to x the function

where the functions and are both continuous in both and in some region of the plane, including, and the functions and are both continuous and both have continuous derivatives for . Then for :

\frac{d}{dx}\,F(x) = f(x,b(x))\,b'(x) - f(x,a(x))\,a'(x) + \int_{a(x)}^{b(x)} \frac{\partial}{\partial x}\, f(x,t)\; dt\,.

This formula is the general form of the Leibniz integral rule and can be derived using the fundamental theorem of calculus. The fundamental theorem of calculus is just a particular case of the above formula, for, a constant, and .

If both upper and lower limits are taken as constants, then the formula takes the shape of an operator equation:

where is the partial derivative with respect to and is the integral operator with respect to over a fixed interval. That is, it is related to the symmetry of second derivatives, but involving integrals as well as derivatives. This case is also known as the Leibniz integral rule.

The following three basic theorems on the interchange of limits are essentially equivalent:

  • the interchange of a derivative and an integral (differentiation under the integral sign; i.e., Leibniz integral rule)
  • the change of order of partial derivatives
  • the change of order of integration (integration under the integral sign; i.e., Fubini's theorem)

Read more about Differentiation Under The Integral Sign:  Higher Dimensions, Derivation of The Principle of Differentiation Under The Integral Sign, Popular Culture

Famous quotes containing the words integral and/or sign:

    “An island always pleases my imagination, even the smallest, as a small continent and integral portion of the globe. I have a fancy for building my hut on one. Even a bare, grassy isle, which I can see entirely over at a glance, has some undefined and mysterious charm for me.”
    —Henry David Thoreau (1817–1862)

    “There is an innocence in lying which is the sign of good faith in a cause.”
    —Friedrich Nietzsche (1844–1900)