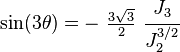Yield Surface - Invariants Used To Describe Yield Surfaces

Invariants Used To Describe Yield Surfaces

The first principal invariant of the Cauchy stress, and the second and third principal invariants of the deviatoric part of the Cauchy stress are defined as:

$\begin{align} I_1 & = \text{Tr}(\boldsymbol{\sigma}) = \sigma_1 + \sigma_2 + \sigma_3 \\ J_2 & = \tfrac{1}{2} \boldsymbol{s}:\boldsymbol{s} = \tfrac{1}{6}\left \\ J_3 & = \det(\boldsymbol{s}) = \tfrac{1}{3} (\boldsymbol{s}\cdot\boldsymbol{s}):\boldsymbol{s} = s_1 s_2 s_3 \end{align}$

where are the principal values of are the principal values of, and

$\boldsymbol{s} = \boldsymbol{\sigma}-\tfrac{I_1}{3}\,\boldsymbol{I}$

where is the identity matrix.

A related set of quantities, are usually used to describe yield surfaces for cohesive frictional materials such as rocks, soils, and ceramics. These are defined as

$p = \tfrac{1}{3}~I_1 ~:~~ q = \sqrt{3~J_2} = \sigma_\mathrm{eq} ~;~~ r = 3\left(\tfrac{1}{2}\,J_3\right)^{1/3}$

where is the equivalent stress. However, the possibility of negative values of and the resulting imaginary makes the use of these quantities problematic in practice.

Another related set of widely used invariants is which describe a cylindrical coordinate system (the Haigh–Westergaard coordinates). These are defined as:

$\xi = \tfrac{1}{\sqrt{3}}~I_1 = \sqrt{3}~p ~;~~ \rho = \sqrt{2 J_2} = \sqrt{\tfrac{2}{3}}~q ~;~~ \cos(3\theta) = \left(\tfrac{r}{q}\right)^3 = \tfrac{3\sqrt{3}}{2}~\cfrac{J_3}{J_2^{3/2}}$

The plane is also called the Rendulic plane. The angle is called the Lode angle and the relation between and was first given by Nayak and Zienkiewicz in 1972

The principal stresses and the Haigh–Westergaard coordinates are related by

$\begin{bmatrix} \sigma_1 \\ \sigma_2 \\ \sigma_3 \end{bmatrix} = \tfrac{1}{\sqrt{3}} \begin{bmatrix} \xi \\ \xi \\ \xi \end{bmatrix} + \sqrt{\tfrac{2}{3}}~\rho~\begin{bmatrix} \cos\theta \\ \cos\left(\theta-\tfrac{2\pi}{3}\right) \\ \cos\left(\theta+\tfrac{2\pi}{3}\right) \end{bmatrix} = \tfrac{1}{\sqrt{3}} \begin{bmatrix} \xi \\ \xi \\ \xi \end{bmatrix} + \sqrt{\tfrac{2}{3}}~\rho~\begin{bmatrix} \cos\theta \\ -\sin\left(\tfrac{\pi}{6}-\theta\right) \\ -\sin\left(\tfrac{\pi}{6}+\theta\right) \end{bmatrix} \,.$

A different definition of the Lode angle can also be found in the literature:

$\sin(3\theta) = -~\tfrac{3\sqrt{3}}{2}~\cfrac{J_3}{J_2^{3/2}}$

in which case

$\begin{bmatrix} \sigma_1 \\ \sigma_2 \\ \sigma_3 \end{bmatrix} = \tfrac{1}{\sqrt{3}} \begin{bmatrix} \xi \\ \xi \\ \xi \end{bmatrix} + \sqrt{\tfrac{2}{3}}~\rho~\begin{bmatrix} \sin\left(\theta-\tfrac{2\pi}{3}\right) \\ \sin\theta \\ \sin\left(\theta+\tfrac{2\pi}{3}\right) \end{bmatrix} = \tfrac{1}{\sqrt{3}} \begin{bmatrix} \xi \\ \xi \\ \xi \end{bmatrix} + \sqrt{\tfrac{2}{3}}~\rho~\begin{bmatrix} -\cos\left(\tfrac{\pi}{6}-\theta\right) \\ \sin\theta \\ \cos\left(\tfrac{\pi}{6}+\theta\right) \end{bmatrix} \,.$

Whatever definition is chosen, the angle varies between 0 degrees to +60 degrees.

Read more about this topic: Yield Surface

Famous quotes containing the words describe, yield and/or surfaces:

“Language was not powerful enough to describe the infant phenomenon. “I’ll tell you what, sir,” he said; “the talent of this child is not to be imagined. She must be seen, sir—seen—to be ever so faintly appreciated.”... The infant phenomenon, though of short stature, had a comparatively aged countenance, and had moreover been precisely the same age—not perhaps to the full extent of the memory of the oldest inhabitant, but certainly for five good years.”
—Charles Dickens (1812–1870)

“I would not deny you; but, by this good day, I yield upon great persuasion; and partly to save your life, for I was told you were in a consumption.”
—William Shakespeare (1564–1616)

“Footnotes are the finer-suckered surfaces that allow tentacular paragraphs to hold fast to the wider reality of the library.”
—Nicholson Baker (b. 1957)