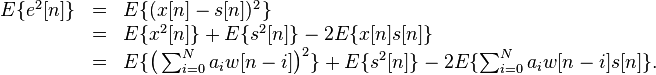Wiener Filter - Finite Impulse Response Wiener Filter For Discrete Series

Finite Impulse Response Wiener Filter For Discrete Series

The causal finite impulse response (FIR) Wiener filter, instead of using some given data matrix X and output vector Y, finds optimal tap weights by using the statistics of the input and output signals. It populates the input matrix X with estimates of the auto-correlation of the input signal (T) and populates the output vector Y with estimates of the cross-correlation between the output and input signals (V).

In order to derive the coefficients of the Wiener filter, consider the signal w being fed to a Wiener filter of order N and with coefficients, . The output of the filter is denoted x which is given by the expression

The residual error is denoted e and is defined as e = x − s (see the corresponding block diagram). The Wiener filter is designed so as to minimize the mean square error (MMSE criteria) which can be stated concisely as follows:

where denotes the expectation operator. In the general case, the coefficients may be complex and may be derived for the case where w and s are complex as well. With a complex signal, the matrix to be solved is a Hermitian Toeplitz matrix, rather than symmetric Toeplitz matrix. For simplicity, the following considers only the case where all these quantities are real. The mean square error (MSE) may be rewritten as:

\begin{array}{rcl} E\{e^2\} &=& E\{(x-s)^2\}\\ &=& E\{x^2\} + E\{s^2\} - 2E\{xs\}\\ &=& E\{\big( \sum_{i=0}^N a_i w \big)^2\} + E\{s^2\} - 2E\{\sum_{i=0}^N a_i ws\} . \end{array}

To find the vector which minimizes the expression above, calculate its derivative with respect to

\begin{array}{rcl} \frac{\partial}{\partial a_i} E\{e^2\} &=& 2E\{ \big( \sum_{j=0}^N a_j w \big) w \} - 2E\{sw\} \quad i=0,\, \ldots,\, N\\ &=& 2 \sum_{j=0}^N E\{ww\} a_j - 2E\{ ws\} . \end{array}

Assuming that w and s are each stationary and jointly stationary, the sequences and known respectively as the autocorrelation of w and the cross-correlation between w and s can be defined as follows:

\begin{align} R_w =& E\{ww\} \\ R_{ws} =& E\{ws\} . \end{align}

The derivative of the MSE may therefore be rewritten as (notice that )

Letting the derivative be equal to zero results in

which can be rewritten in matrix form

\begin{align} &\mathbf{T}\mathbf{a} = \mathbf{v}\\ \Rightarrow &\begin{bmatrix} R_w & R_w & \cdots & R_w \\ R_w & R_w & \cdots & R_w \\ \vdots & \vdots & \ddots & \vdots \\ R_w & R_w & \cdots & R_w \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_N \end{bmatrix} = \begin{bmatrix} R_{sw} \\R_{sw} \\ \vdots \\ R_{sw} \end{bmatrix} \end{align}

These equations are known as the Wiener–Hopf equations. The matrix T appearing in the equation is a symmetric Toeplitz matrix. These matrices are known to be positive definite and therefore non-singular yielding a unique solution to the determination of the Wiener filter coefficient vector, . Furthermore, there exists an efficient algorithm to solve such Wiener–Hopf equations known as the Levinson-Durbin algorithm so an explicit inversion of is not required.

Read more about this topic:  Wiener Filter

Famous quotes containing the words finite, impulse, response, wiener, discrete and/or series:

    “The finite is annihilated in the presence of the infinite, and becomes a pure nothing. So our spirit before God, so our justice before divine justice.”
    —Blaise Pascal (1623–1662)

    “There are moods in which one feels the impulse to enter a tacit protest against too gross an appetite for pure aesthetics in this starving and sinning world. One turns half away, musingly, from certain beautiful useless things.”
    —Henry James (1843–1916)

    “The reason can give nothing at all Like the response to desire.”
    —Wallace Stevens (1879–1955)

    “The idea that information can be stored in a changing world without an overwhelming depreciation of its value is false. It is scarcely less false than the more plausible claim that after a war we may take our existing weapons, fill their barrels with cylinder oil, and coat their outsides with sprayed rubber film, and let them statically await the next emergency.”
    —Norbert Wiener (1894–1964)

    “One can describe a landscape in many different words and sentences, but one would not normally cut up a picture of a landscape and rearrange it in different patterns in order to describe it in different ways. Because a photograph is not composed of discrete units strung out in a linear row of meaningful pieces, we do not understand it by looking at one element after another in a set sequence. The photograph is understood in one act of seeing; it is perceived in a gestalt.”
    —Joshua Meyrowitz, U.S. educator, media critic. “The Blurring of Public and Private Behaviors,” No Sense of Place: The Impact of Electronic Media on Social Behavior, Oxford University Press (1985)

    “I look on trade and every mechanical craft as education also. But let me discriminate what is precious herein. There is in each of these works an act of invention, an intellectual step, or short series of steps taken; that act or step is the spiritual act; all the rest is mere repetition of the same a thousand times.”
    —Ralph Waldo Emerson (1803–1882)