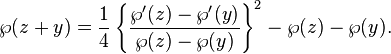Weierstrass's Elliptic Functions - Addition Theorems

Addition Theorems

The Weierstrass elliptic functions have several properties that may be proved:

\det\begin{bmatrix} \wp(z) & \wp'(z) & 1\\ \wp(y) & \wp'(y) & 1\\ \wp(z+y) & -\wp'(z+y) & 1 \end{bmatrix}=0

(a symmetrical version would be

\det\begin{bmatrix} \wp(u) & \wp'(u) & 1\\ \wp(v) & \wp'(v) & 1\\ \wp(w) & \wp'(w) & 1 \end{bmatrix}=0

where u + v + w = 0).

Also

\wp(z+y)=\frac{1}{4} \left\{ \frac{\wp'(z)-\wp'(y)}{\wp(z)-\wp(y)} \right\}^2 -\wp(z)-\wp(y).

and the duplication formula

\wp(2z)= \frac{1}{4}\left\{ \frac{\wp''(z)}{\wp'(z)}\right\}^2-2\wp(z),

unless 2z is a period.

Read more about this topic:  Weierstrass's Elliptic Functions

Famous quotes containing the word addition:

    “But the best read naturalist who lends an entire and devout attention to truth, will see that there remains much to learn of his relation to the world, and that it is not to be learned by any addition or subtraction or other comparison of known quantities, but is arrived at by untaught sallies of the spirit, by a continual self-recovery, and by entire humility.”
    —Ralph Waldo Emerson (1803–1882)