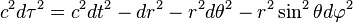Two-body Problem in General Relativity - General Relativity, Special Relativity and Geometry | General Relativity, Special Relativity Geometry

General Relativity, Special Relativity and Geometry

In the normal Euclidean geometry, triangles obey the Pythagorean theorem, which states that the square distance ds2 between two points in space is the sum of the squares of its perpendicular components

$ds^{2} = dx^{2} + dy^{2} + dz^{2} \,\!$

where dx, dy and dz represent the infinitesimal differences between the two points along the x, y and z axes of a Cartesian coordinate system (add Figure here). Now imagine a world in which this is not quite true; a world where the distance is instead given by

$ds^{2} = F(x, y, z) dx^{2} + G(x, y, z) dy^{2} + H(x, y, z)dz^{2} \,\!$

where F, G and H are arbitrary functions of position. It is not hard to imagine such a world; we live on one. The surface of the world is curved, which is why it's impossible to make a perfectly accurate flat map of the world. Non-Cartesian coordinate systems illustrate this well; for example, in the spherical coordinates (r, θ, φ), the Euclidean distance can be written

$ds^{2} = dr^{2} + r^{2} d\theta^{2} + r^{2} \sin^{2} \theta d\varphi^{2} \,\!$

Another illustration would be a world in which the rulers used to measure length were untrustworthy, rulers that changed their length with their position and even their orientation. In the most general case, one must allow for cross-terms when calculating the distance ds

$ds^{2} = g_{xx} dx^{2} + g_{xy} dx dy + g_{xz} dx dz + \cdots + g_{zy} dz dy + g_{zz} dz^{2} \,\!$

where the nine functions g_xx, g_xy constitute the metric tensor, which defines the geometry of the space in Riemannian geometry. In the spherical-coordinates example above, there are no cross-terms; the only nonzero metric tensor components are g_rr = 1, g_θθ = r2 and g_φφ = r2 sin2 θ.

In his special theory of relativity, Albert Einstein showed that the distance ds between two spatial points is not constant, but depends on the motion of the observer. However, there is a measure of separation between two points in space-time — called "proper time" and denoted with the symbol dτ — that is invariant; in other words, it doesn't depend on the motion of the observer.

$c^{2} d\tau^{2} = c^{2} dt^{2} - dx^{2} - dy^{2} - dz^{2} \,\!$

which may be written in spherical coordinates as

$c^{2} d\tau^{2} = c^{2} dt^{2} - dr^{2} - r^{2} d\theta^{2} - r^{2} \sin^{2} \theta d\varphi^{2} \,\!$

This formula is the natural extension of the Pythagorean theorem and similarly holds only when there is no curvature in space-time. In general relativity, however, space and time may have curvature, so this distance formula must be modified to a more general form

$c^{2} d\tau^{2} = g_{\mu\nu} dx^{\mu} dx^{\nu} \,\!$

just as we generalized the formula to measure distance on the surface of the Earth. The exact form of the metric g_μν depends on the gravitating mass, momentum and energy, as described by the Einstein field equations. Einstein developed those field equations to match the then known laws of Nature; however, they predicted never-before-seen phenomena (such as the bending of light by gravity) that were confirmed later.

Read more about this topic: Two-body Problem In General Relativity

Famous quotes containing the words general, special, relativity and/or geometry:

“The man who would change the name of Arkansas is the original, iron-jawed, brass-mouthed, copper-bellied corpse-maker from the wilds of the Ozarks! He is the man they call Sudden Death and General Desolation! Sired by a hurricane, dam’d by an earthquake, half-brother to the cholera, nearly related to the smallpox on his mother’s side!”
—Administration in the State of Arka, U.S. public relief program (1935-1943)

“Beauty, like all other qualities presented to human experience, is relative; and the definition of it becomes unmeaning and useless in proportion to its abstractness. To define beauty not in the most abstract, but in the most concrete terms possible, not to find a universal formula for it, but the formula which expresses most adequately this or that special manifestation of it, is the aim of the true student of aesthetics.”
—Walter Pater (1839–1894)

“By an application of the theory of relativity to the taste of readers, to-day in Germany I am called a German man of science, and in England I am represented as a Swiss Jew. If I come to be regarded as a bête noire the descriptions will be reversed, and I shall become a Swiss Jew for the Germans and a German man of science for the English!”
—Albert Einstein (1879–1955)

“I am present at the sowing of the seed of the world. With a geometry of sunbeams, the soul lays the foundations of nature.”
—Ralph Waldo Emerson (1803–1882)