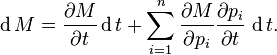Total Derivative - The Total Derivative Via Differentials

The Total Derivative Via Differentials

Differentials provide a simple way to understand the total derivative. For instance, suppose is a function of time t and n variables as in the previous section. Then, the differential of M is

This expression is often interpreted heuristically as a relation between infinitesimals. However, if the variables t and pj are interpreted as functions, and is interpreted to mean the composite of M with these functions, then the above expression makes perfect sense as an equality of differential 1-forms, and is immediate from the chain rule for the exterior derivative. The advantage of this point of view is that it takes into account arbitrary dependencies between the variables. For example, if then . In particular, if the variables pj are all functions of t, as in the previous section, then

\operatorname d M = \frac{\partial M}{\partial t} \operatorname d t + \sum_{i=1}^n \frac{\partial M}{\partial p_i}\frac{\partial p_i}{\partial t}\,\operatorname d t.

Read more about this topic:  Total Derivative

Famous quotes containing the words total and/or derivative:

    “The human spirit is itself the most wonderful fairy tale that can possibly be. What a magnificent world lies enclosed within our bosoms! No solar orbit hems it in, the inexhaustible wealth of the total visible creation is outweighed by its riches!”
    —E.T.A.W. (Ernst Theodor Amadeus Wilhelm)

    “When we say “science” we can either mean any manipulation of the inventive and organizing power of the human intellect: or we can mean such an extremely different thing as the religion of science the vulgarized derivative from this pure activity manipulated by a sort of priestcraft into a great religious and political weapon.”
    —Wyndham Lewis (1882–1957)