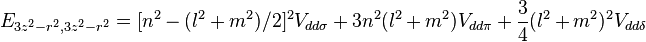Tight Binding - Table of Interatomic Matrix Elements

Table of Interatomic Matrix Elements

In 1954 J.C. Slater and F.G. Koster published, mainly for the calculation of transition metal d-bands, a table of interatomic matrix elements

which, with a little patience and effort, can also be derived from the cubic harmonic orbitals straightforwardly. The table expresses the matrix elements as functions of LCAO two-centre bond integrals between two cubic harmonic orbitals, i and j, on adjacent atoms. The bond integrals are for example the, and for sigma, pi and delta bonds.

The interatomic vector is expressed as

where d is the distance between the atoms and l, m and n are the direction cosines to the neighboring atom.

E_{x,x^2-y^2} = \frac{\sqrt{3}}{2} l (l^2 - m^2) V_{pd\sigma} + l (1 - l^2 + m^2) V_{pd\pi}
E_{y,x^2-y^2} = \frac{\sqrt{3}}{2} m(l^2 - m^2) V_{pd\sigma} - m (1 + l^2 - m ^2) V_{pd\pi}
E_{z,3z^2-r^2} = n V_{pd\sigma} + \sqrt{3} n (l^2 + m^2) V_{pd\pi}
E_{xy,xy} = 3 l^2 m^2 V_{dd\sigma} + (l^2 + m^2 - 4 l^2 m^2) V_{dd\pi} + (n^2 + l^2 m^2) V_{dd\delta}
E_{xy,yz} = 3 l m^2 nV_{dd\sigma} + l n (1 - 4 m^2) V_{dd\pi} + l n (m^2 - 1) V_{dd\delta}
E_{xy,zx} = 3 l^2 m n V_{dd\sigma} + m n (1 - 4 l^2) V_{dd\pi} + m n (l^2 - 1) V_{dd\delta}
E_{xy,x^2-y^2} = \frac{3}{2} l m (l^2 - m^2) V_{dd\sigma} + 2 l m (m^2 - l^2) V_{dd\pi} + l m (l^2 - m^2) / 2 V_{dd\delta}
E_{yz,x^2-y^2} = \frac{3}{2} m n (l^2 - m^2) V_{dd\sigma} - m n V_{dd\pi} + m n V_{dd\delta}
E_{zx,x^2-y^2} = \frac{3}{2} n l (l^2 - m^2) V_{dd\sigma} + n l V_{dd\pi} - n l V_{dd\delta}
E_{xy,3z^2-r^2} = \sqrt{3} \left[ l m (n^2 - (l^2 + m^2) / 2) V_{dd\sigma} - 2 l m n^2 V_{dd\pi} + l m (1 + n^2) / 2 V_{dd\delta} \right]
E_{yz,3z^2-r^2} = \sqrt{3} \left[ m n (n^2 - (l^2 + m^2) / 2) V_{dd\sigma} + m n (l^2 + m^2 - n^2) V_{dd\pi} - m n (l^2 + m^2) / 2 V_{dd\delta} \right]
E_{zx,3z^2-r^2} = \sqrt{3} \left[ l n (n^2 - (l^2 + m^2) / 2) V_{dd\sigma} + l n (l^2 + m^2 - n^2) V_{dd\pi} - l n (l^2 + m^2) / 2 V_{dd\delta} \right]
E_{x^2-y^2,x^2-y^2} = \frac{3}{4} (l^2 - m^2)^2 V_{dd\sigma} + V_{dd\pi} + V_{dd\delta}
E_{x^2-y^2,3z^2-r^2} = \sqrt{3} \left[ (l^2 - m^2) V_{dd\sigma} / 2 + n^2 (m^2 - l^2) V_{dd\pi} + (1 + n^2)(l^2 - m^2) / 4 V_{dd\delta}\right]
E_{3z^2-r^2,3z^2-r^2} = ^2 V_{dd\sigma} + 3 n^2 (l^2 + m^2) V_{dd\pi} + \frac{3}{4} (l^2 + m^2)^2 V_{dd\delta}

Not all interatomic matrix elements are listed explicitly. Matrix elements that are not listed in this table can be constructed by permutation of indices and cosine directions of other matrix elements in the table.

Read more about this topic:  Tight Binding

Famous quotes containing the words table, matrix and/or elements:

    “A big leather-bound volume makes an ideal razorstrap. A thin book is useful to stick under a table with a broken caster to steady it. A large, flat atlas can be used to cover a window with a broken pane. And a thick, old-fashioned heavy book with a clasp is the finest thing in the world to throw at a noisy cat.”
    —Mark Twain [Samuel Langhorne Clemens] (1835–1910)

    “In all cultures, the family imprints its members with selfhood. Human experience of identity has two elements; a sense of belonging and a sense of being separate. The laboratory in which these ingredients are mixed and dispensed is the family, the matrix of identity.”
    —Salvador Minuchin (20th century)

    “The elements of success in this business do not differ from the elements of success in any other. Competition is keen and bitter. Advertising is as large an element as in any other business, and since the usual avenues of successful exploitation are closed to the profession, the adage that the best advertisement is a pleased customer is doubly true for this business.”
    —Madeleine [Blair], U.S. prostitute and “madam.” Madeleine, ch. 5 (1919)