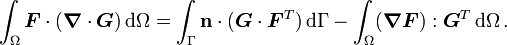Tensor Derivative (continuum Mechanics) - Integration By Parts

Integration By Parts

Another important operation related to tensor derivatives in continuum mechanics is integration by parts. The formula for integration by parts can be written as

$\int_{\Omega} \boldsymbol{F}\otimes\boldsymbol{\nabla}\boldsymbol{G}\,{\rm d}\Omega = \int_{\Gamma} \mathbf{n}\otimes(\boldsymbol{F}\otimes\boldsymbol{G})\,{\rm d}\Gamma - \int_{\Omega} \boldsymbol{G}\otimes\boldsymbol{\nabla}\boldsymbol{F}\,{\rm d}\Omega$

where and are differentiable tensor fields of arbitrary order, is the unit outward normal to the domain over which the tensor fields are defined, represents a generalized tensor product operator, and is a generalized gradient operator. When is equal to the identity tensor, we get the divergence theorem

$\int_{\Omega}\boldsymbol{\nabla}\boldsymbol{G}\,{\rm d}\Omega = \int_{\Gamma} \mathbf{n}\otimes\boldsymbol{G}\,{\rm d}\Gamma \,.$

We can express the formula for integration by parts in Cartesian index notation as

$\int_{\Omega} F_{ijk....}\,G_{lmn...,p}\,{\rm d}\Omega = \int_{\Gamma} n_p\,F_{ijk...}\,G_{lmn...}\,{\rm d}\Gamma - \int_{\Omega} G_{lmn...}\,F_{ijk...,p}\,{\rm d}\Omega \,.$

For the special case where the tensor product operation is a contraction of one index and the gradient operation is a divergence, and both and are second order tensors, we have

$\int_{\Omega} \boldsymbol{F}\cdot(\boldsymbol{\nabla}\cdot\boldsymbol{G})\,{\rm d}\Omega = \int_{\Gamma} \mathbf{n}\cdot(\boldsymbol{G}\cdot\boldsymbol{F}^T)\,{\rm d}\Gamma - \int_{\Omega} (\boldsymbol{\nabla}\boldsymbol{F}):\boldsymbol{G}^T\,{\rm d}\Omega \,.$

In index notation,

$\int_{\Omega} F_{ij}\,G_{pj,p}\,{\rm d}\Omega = \int_{\Gamma} n_p\,F_{ij}\,G_{pj}\,{\rm d}\Gamma - \int_{\Omega} G_{pj}\,F_{ij,p}\,{\rm d}\Omega \,.$

Read more about this topic: Tensor Derivative (continuum Mechanics)

Famous quotes containing the words integration and/or parts:

“The more specific idea of evolution now reached is—a change from an indefinite, incoherent homogeneity to a definite, coherent heterogeneity, accompanying the dissipation of motion and integration of matter.”
—Herbert Spencer (1820–1903)

“She, as a veil down to the slender waist,
Her unadorned golden tresses wore
Dishevelled, but in wanton ringlets waved
As the vine curls her tendrils, which implied
Subjection, but required with gentle sway,
And by her yielded, by him best received,
Yielded with coy submission, modest pride,
And sweet, reluctant, amorous delay.
Nor those mysterious parts were then concealed:
Then was not guilty shame: dishonest Shame
Of Nature’s works, Honour dishonourable.”
—John Milton (1608–1674)