Derivatives of The Invariants of A Second-order Tensor
The principal invariants of a second order tensor are
The derivatives of these three invariants with respect to are
-
Proof From the derivative of the determinant we know that For the derivatives of the other two invariants, let us go back to the characteristic equation
Using the same approach as for the determinant of a tensor, we can show that
Now the left hand side can be expanded as
Hence
or,
Expanding the right hand side and separating terms on the left hand side gives
or,
If we define and, we can write the above as
Collecting terms containing various powers of λ, we get
Then, invoking the arbitrariness of λ, we have
This implies that
Read more about this topic: Tensor Derivative (continuum Mechanics)

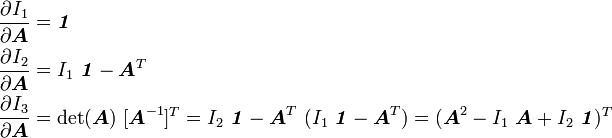


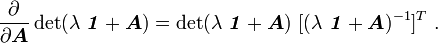
![\begin{align} \frac{\partial }{\partial \boldsymbol{A}}\det(\lambda~\boldsymbol{\mathit{1}} + \boldsymbol{A}) & = \frac{\partial }{\partial \boldsymbol{A}}\left[ \lambda^3 + I_1(\boldsymbol{A})~\lambda^2 + I_2(\boldsymbol{A})~\lambda + I_3(\boldsymbol{A}) \right] \\ & = \frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + \frac{\partial I_3}{\partial \boldsymbol{A}}~. \end{align}](http://upload.wikimedia.org/math/0/c/c/0cccee2c6790ad09f86a08f7d515f21c.png)

![(\lambda~\boldsymbol{\mathit{1}}+\boldsymbol{A})^T\cdot\left[ \frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + \frac{\partial I_3}{\partial \boldsymbol{A}}\right] = \det(\lambda~\boldsymbol{\mathit{1}} + \boldsymbol{A})~\boldsymbol{\mathit{1}} ~.](http://upload.wikimedia.org/math/d/9/9/d99fe1fc70f607dca5765ec2190fc027.png)
![(\lambda~\boldsymbol{\mathit{1}} +\boldsymbol{A}^T)\cdot\left[ \frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + \frac{\partial I_3}{\partial \boldsymbol{A}}\right] = \left \boldsymbol{\mathit{1}}](http://upload.wikimedia.org/math/8/9/d/89df0f22b98b33ed82ca716de7a9b37b.png)
![\begin{align} \left[\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^3 \right.& \left.+ \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_3}{\partial \boldsymbol{A}}~\lambda\right]\boldsymbol{\mathit{1}} + \boldsymbol{A}^T\cdot\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \boldsymbol{A}^T\cdot\frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + \boldsymbol{A}^T\cdot\frac{\partial I_3}{\partial \boldsymbol{A}} \\ & = \left \boldsymbol{\mathit{1}} ~. \end{align}](http://upload.wikimedia.org/math/c/3/8/c388c8b7cc3c8fad584f8ac00da12fe4.png)
![\begin{align} \left[\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^3 \right.& \left.+ \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_3}{\partial \boldsymbol{A}}~\lambda + \frac{\partial I_4}{\partial \boldsymbol{A}}\right]\boldsymbol{\mathit{1}} + \boldsymbol{A}^T\cdot\frac{\partial I_0}{\partial \boldsymbol{A}}~\lambda^3 + \boldsymbol{A}^T\cdot\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \boldsymbol{A}^T\cdot\frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + \boldsymbol{A}^T\cdot\frac{\partial I_3}{\partial \boldsymbol{A}} \\ &= \left \boldsymbol{\mathit{1}} ~. \end{align}](http://upload.wikimedia.org/math/0/4/f/04fbec4739fd8c111c00fb290a91b288.png)


