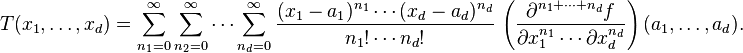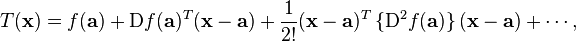Taylor Series - Taylor Series in Several Variables

Taylor Series in Several Variables

The Taylor series may also be generalized to functions of more than one variable with

T(x_1,\dots,x_d) = \sum_{n_1=0}^\infty \sum_{n_2=0}^\infty \cdots \sum_{n_d = 0}^\infty \frac{(x_1-a_1)^{n_1}\cdots (x_d-a_d)^{n_d}}{n_1!\cdots n_d!}\,\left(\frac{\partial^{n_1 + \cdots + n_d}f}{\partial x_1^{n_1}\cdots \partial x_d^{n_d}}\right)(a_1,\dots,a_d).\!

For example, for a function that depends on two variables, x and y, the Taylor series to second order about the point (a, b) is:

\begin{align} f(x,y) & \approx f(a,b) +(x-a)\, f_x(a,b) +(y-b)\, f_y(a,b) \\ & {}\quad + \frac{1}{2!}\left, \end{align}

where the subscripts denote the respective partial derivatives.

A second-order Taylor series expansion of a scalar-valued function of more than one variable can be written compactly as

T(\mathbf{x}) = f(\mathbf{a}) + \mathrm{D} f(\mathbf{a})^T (\mathbf{x} - \mathbf{a}) + \frac{1}{2!} (\mathbf{x} - \mathbf{a})^T \,\{\mathrm{D}^2 f(\mathbf{a})\}\,(\mathbf{x} - \mathbf{a}) + \cdots\! \,,

where is the gradient of evaluated at and is the Hessian matrix. Applying the multi-index notation the Taylor series for several variables becomes

which is to be understood as a still more abbreviated multi-index version of the first equation of this paragraph, again in full analogy to the single variable case.

Read more about this topic:  Taylor Series

Famous quotes containing the words taylor, series and/or variables:

    “An orphan’s curse would drag to hell
    A spirit from on high;
    But oh! more horrible than that
    Is a curse in a dead man’s eye!”
    —Samuel Taylor Coleridge (1772–1834)

    “The theory of truth is a series of truisms.”
    —J.L. (John Langshaw)

    “Science is feasible when the variables are few and can be enumerated; when their combinations are distinct and clear. We are tending toward the condition of science and aspiring to do it. The artist works out his own formulas; the interest of science lies in the art of making science.”
    —Paul Valéry (1871–1945)