Stress Functions - Beltrami Stress Functions

Beltrami Stress Functions

It can be shown that a complete solution to the equilibrium equations may be written as

Using index notation:

Engineering notation
\sigma_x = \frac{\partial^2\Phi_{yy}}{\partial z \partial z} + \frac{\partial^2\Phi_{zz}}{\partial y \partial y} -2\frac{\partial^2\Phi_{yz}}{\partial y \partial z} \sigma_{xy} =-\frac{\partial^2\Phi_{xy}}{\partial z \partial z} -\frac{\partial^2\Phi_{zz}}{\partial x \partial y} +\frac{\partial^2\Phi_{yz}}{\partial x \partial z} +\frac{\partial^2\Phi_{zx}}{\partial y \partial z}
\sigma_y = \frac{\partial^2\Phi_{xx}}{\partial z \partial z} +\frac{\partial^2\Phi_{zz}}{\partial x \partial x} -2\frac{\partial^2\Phi_{zx}}{\partial z \partial x} \sigma_{yz} =-\frac{\partial^2\Phi_{yz}}{\partial x \partial x} -\frac{\partial^2\Phi_{xx}}{\partial y \partial z} +\frac{\partial^2\Phi_{zx}}{\partial y \partial x} +\frac{\partial^2\Phi_{xy}}{\partial z \partial x}
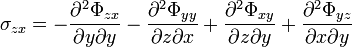
\sigma_z = \frac{\partial^2\Phi_{yy}}{\partial x \partial x} +\frac{\partial^2\Phi_{xx}}{\partial y \partial y} -2\frac{\partial^2\Phi_{xy}}{\partial x \partial y} \sigma_{zx} =-\frac{\partial^2\Phi_{zx}}{\partial y \partial y} -\frac{\partial^2\Phi_{yy}}{\partial z \partial x} +\frac{\partial^2\Phi_{xy}}{\partial z \partial y} +\frac{\partial^2\Phi_{yz}}{\partial x \partial y}

where is an arbitrary second-rank tensor field that is continuously differentiable at least four times, and is known as the Beltrami stress tensor. Its components are known as Beltrami stress functions. is the Levi-Civita pseudotensor, with all values equal to zero except those in which the indices are not repeated. For a set of non-repeating indices the component value will be +1 for even permutations of the indices, and -1 for odd permutations. And is the Nabla operator

Read more about this topic:  Stress Functions

Famous quotes containing the words stress and/or functions:

    “A society which is clamoring for choice, which is filled with many articulate groups, each urging its own brand of salvation, its own variety of economic philosophy, will give each new generation no peace until all have chosen or gone under, unable to bear the conditions of choice. The stress is in our civilization.”
    —Margaret Mead (1901–1978)

    “The English masses are lovable: they are kind, decent, tolerant, practical and not stupid. The tragedy is that there are too many of them, and that they are aimless, having outgrown the servile functions for which they were encouraged to multiply. One day these huge crowds will have to seize power because there will be nothing else for them to do, and yet they neither demand power nor are ready to make use of it; they will learn only to be bored in a new way.”
    —Cyril Connolly (1903–1974)