Stiff Equation - Stiffness Ratio

Stiffness Ratio

Consider the linear constant coefficient inhomogeneous system

where and is a constant matrix with eigenvalues (assumed distinct) and corresponding eigenvectors . The general solution of (5) takes the form

$\bold y(x) = \sum_{t=1}^{n} \kappa_t \exp ( \lambda_t x ) \bold c_t + \bold g(x), \qquad (6)$

where the κ_t are arbitrary constants and is a particular integral. Now let us suppose that

$Re(\lambda_t) < 0, \qquad t = 1, 2, \ldots, n, \qquad \quad (7)$

which implies that each of the terms as, so that the solution approaches asymptotically as ; the term will decay monotonically if λ_t is real and sinusoidally if λ_t is complex. Interpreting x to be time (as it often is in physical problems) it is appropriate to call the transient solution and the steady-state solution. If is large, then the corresponding term will decay quickly as x increases and is thus called a fast transient; if is small, the corresponding term decays slowly and is called a slow transient. Let 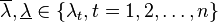$\overline{\lambda}, \underline{\lambda} \in \{ \lambda_t, t = 1, 2, \ldots, n \}$ be defined by

$| Re( \overline{\lambda} ) | \geq | Re( \lambda_t ) | \geq | Re( \underline{\lambda} ) |, \qquad t = 1, 2, \ldots, n \qquad (8)$

so that is the fastest transient and the slowest. We now define the stiffness ratio as

$\frac{ | Re( \overline{\lambda} ) | } { | Re( \underline{\lambda} ) | }. \qquad \qquad \qquad \qquad \qquad \qquad \quad (9)$

Read more about this topic: Stiff Equation

Famous quotes containing the words stiffness and/or ratio:

“Everything ponderous, viscous, and solemnly clumsy, all long- winded and boring types of style are developed in profuse variety among Germans—forgive me the fact that even Goethe’s prose, in its mixture of stiffness and elegance, is no exception, being a reflection of the “good old time” to which it belongs, and a reflection of German taste at a time when there still was a “German taste”Ma rococo taste in moribus et artibus.”
—Friedrich Nietzsche (1844–1900)

“A magazine or a newspaper is a shop. Each is an experiment and represents a new focus, a new ratio between commerce and intellect.”
—John Jay Chapman (1862–1933)