Relation Between Pauli Group and Binary Vectors
A simple but useful mapping exists between elements of and the binary vector space . This mapping gives a simplification of quantum error correction theory. It represents quantum codes with binary vectors and binary operations rather than with Pauli operators and matrix operations respectively.
We first give the mapping for the one-qubit case. Suppose is a set of equivalence classes of an operator that have the same phase:
Let be the set of phase-free Pauli operators where . Define the map as
Suppose . Let us employ the shorthand and  where, . For example, suppose . Then . The map induces an isomorphism
where, . For example, suppose . Then . The map induces an isomorphism  because addition of vectors in is equivalent to multiplication of Pauli operators up to a global phase:
because addition of vectors in is equivalent to multiplication of Pauli operators up to a global phase:
Let denote the symplectic product between two elements  :
:
The symplectic product gives the commutation relations of elements of :
The symplectic product and the mapping thus give a useful way to phrase Pauli relations in terms of binary algebra. The extension of the above definitions and mapping to multiple qubits is straightforward. Let denote an arbitrary element of . We can similarly define the phase-free -qubit Pauli group ![\left =\left\{ \left[
\mathbf{A}\right] \ |\ \mathbf{A}\in\Pi^{n}\right\}](http://upload.wikimedia.org/math/f/d/c/fdc34c668a5b5aaeb99df053d5bbf930.png) where
where
The group operation for the above equivalence class is as follows:
The equivalence class forms a commutative group under operation . Consider the -dimensional vector space
It forms the commutative group with operation defined as binary vector addition. We employ the notation  to represent any vectors respectively. Each vector and has elements
to represent any vectors respectively. Each vector and has elements 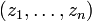 and respectively with similar representations for and . The \textit{symplectic product} of and is
and respectively with similar representations for and . The \textit{symplectic product} of and is
or
where and  . Let us define a map
. Let us define a map  as follows:
as follows:
Let
so that and  belong to the same equivalence class:
belong to the same equivalence class:
The map  is an isomorphism for the same reason given as the previous case:
is an isomorphism for the same reason given as the previous case:
where . The symplectic product captures the commutation relations of any operators 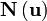 and :
and :
The above binary representation and symplectic algebra are useful in making the relation between classical linear error correction and quantum error correction more explicit.
Read more about this topic: Stabilizer Code
Famous quotes containing the words relation between, relation and/or group:
“We shall never resolve the enigma of the relation between the negative foundations of greatness and that greatness itself.”
—Jean Baudrillard (b. 1929)
“You know there are no secrets in America. It’s quite different in England, where people think of a secret as a shared relation between two people.”
—W.H. (Wystan Hugh)
“No group and no government can properly prescribe precisely what should constitute the body of knowledge with which true education is concerned.”
—Franklin D. Roosevelt (1882–1945)






![\left \ast\left \equiv\left[
A_{1}\right] \ast\left \otimes\cdots\otimes\left[
A_{n}\right] \ast\left =\left \otimes\cdots\otimes\left
=\left .](http://upload.wikimedia.org/math/f/a/d/fad33c795c8368f0e7dd7c443ad64b4f.png)




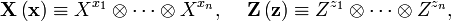
![\left =\left[ \mathbf{Z}
\left( \mathbf{z}\right) \mathbf{X}\left( \mathbf{x}\right) \right] .](http://upload.wikimedia.org/math/0/f/3/0f340def5f6a649a2d091edf896a8e2c.png)
![\left =\left[
\mathbf{N}\left( \mathbf{u}\right) \right] \left[ \mathbf{N}\left(
\mathbf{v}\right) \right] ,](http://upload.wikimedia.org/math/4/c/f/4cffab8f2ba98b46c43a111634b0a656.png)
