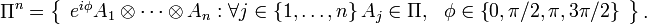Stabilizer Code - Mathematical Background

Mathematical Background

The Stabilizer formalism exploits elements of the Pauli group in formulating quantum error-correcting codes. The set consists of the Pauli operators:

I\equiv \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} ,\ X\equiv \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} ,\ Y\equiv \begin{bmatrix} 0 & -i\\ i & 0 \end{bmatrix} ,\ Z\equiv \begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix} .

The above operators act on a single qubit---a state represented by a vector in a two-dimensional Hilbert space. Operators in have eigenvalues and either commute or anti-commute. The set consists of -fold tensor products of Pauli operators:

\Pi^{n}=\left\{ \begin{array} {c} e^{i\phi}A_{1}\otimes\cdots\otimes A_{n}:\forall j\in\left\{ 1,\ldots ,n\right\} A_{j}\in\Pi,\ \ \phi\in\left\{ 0,\pi/2,\pi,3\pi/2\right\} \end{array} \right\} .

Elements of act on a quantum register of qubits. We occasionally omit tensor product symbols in what follows so that

The -fold Pauli group plays an important role for both the encoding circuit and the error-correction procedure of a quantum stabilizer code over qubits.

Read more about this topic:  Stabilizer Code

Famous quotes containing the words mathematical and/or background:

    “All science requires mathematics. The knowledge of mathematical things is almost innate in us.... This is the easiest of sciences, a fact which is obvious in that no one’s brain rejects it; for laymen and people who are utterly illiterate know how to count and reckon.”
    —Roger Bacon (c. 1214–c. 1294)

    “They were more than hostile. In the first place, I was a south Georgian and I was looked upon as a fiscal conservative, and the Atlanta newspapers quite erroneously, because they didn’t know anything about me or my background here in Plains, decided that I was also a racial conservative.”
    —Jimmy Carter (James Earl Carter, Jr.)