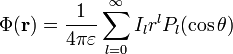Spherical Multipole Moments - Special Case of Axial Symmetry

Special Case of Axial Symmetry

The spherical multipole expansion takes a simple form if the charge distribution is axially symmetric (i.e., is independent of the azimuthal angle ). By carrying out the integrations that define and, it can be shown the multipole moments are all zero except when . Using the mathematical identity

P_{l}(\cos \theta) \ \stackrel{\mathrm{def}}{=}\ \sqrt{\frac{4\pi}{2l+1}} Y_{l0}(\theta, \phi)

the exterior multipole expansion becomes

\Phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon} \sum_{l=0}^{\infty} \left( \frac{Q_{l}}{r^{l+1}} \right) P_{l}(\cos \theta)

where the axially symmetric multipole moments are defined

Q_{l} \ \stackrel{\mathrm{def}}{=}\ \int d\mathbf{r}^{\prime} \rho(\mathbf{r}^{\prime}) \left( r^{\prime} \right)^{l} P_{l}(\cos \theta^{\prime})

In the limit that the charge is confined to the -axis, we recover the exterior axial multipole moments.

Similarly the interior multipole expansion becomes

\Phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon} \sum_{l=0}^{\infty} I_{l} r^{l} P_{l}(\cos \theta)

where the axially symmetric interior multipole moments are defined

I_{l} \ \stackrel{\mathrm{def}}{=}\ \int d\mathbf{r}^{\prime} \frac{\rho(\mathbf{r}^{\prime})}{\left( r^{\prime} \right)^{l+1}} P_{l}(\cos \theta^{\prime})

In the limit that the charge is confined to the -axis, we recover the interior axial multipole moments.

Read more about this topic:  Spherical Multipole Moments

Famous quotes containing the words special, case and/or symmetry:

    “... there has been a very special man in my life for the past year. All I’ll say about him is that he’s kind, warm, mature, someone I can trust—and he’s not a politician.”
    —Donna Rice (b. c. 1962)

    “My case is a species of madness, only that it is a derangement of the Volition, & not of the intellectual faculties.”
    —Samuel Taylor Coleridge (1772–1834)

    “What makes a regiment of soldiers a more noble object of view than the same mass of mob? Their arms, their dresses, their banners, and the art and artificial symmetry of their position and movements.”
    —George Gordon Noel Byron (1788–1824)