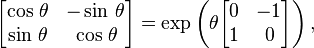Skew-symmetric Matrix - Infinitesimal Rotations

Infinitesimal Rotations

Skew-symmetric matrices over the field of real numbers form the tangent space to the real orthogonal group O(n) at the identity matrix; formally, the special orthogonal Lie algebra. In this sense, then, skew-symmetric matrices can be thought of as infinitesimal rotations.

Another way of saying this is that the space of skew-symmetric matrices forms the Lie algebra o(n) of the Lie group O(n). The Lie bracket on this space is given by the commutator:

It is easy to check that the commutator of two skew-symmetric matrices is again skew-symmetric:

The matrix exponential of a skew-symmetric matrix A is then an orthogonal matrix R:

The image of the exponential map of a Lie algebra always lies in the connected component of the Lie group that contains the identity element. In the case of the Lie group O(n), this connected component is the special orthogonal group SO(n), consisting of all orthogonal matrices with determinant 1. So R = exp(A) will have determinant +1. Moreover, since the exponential map of a connected compact Lie group is always surjective, it turns out that every orthogonal matrix with unit determinant can be written as the exponential of some skew-symmetric matrix. In the particular important case of dimension n=2, the exponential representation for an orthogonal matrix reduces to the well-known polar form of a complex number of unit modulus. Indeed, if n=2, a special orthogonal matrix has the form

with a2+b2=1. Therefore, putting a=cosθ and b=sinθ, it can be written

which corresponds exactly to the polar form cosθ + isinθ = eiθ of a complex number of unit modulus. The exponential representation of an orthogonal matrix of order n can also be obtained starting from the fact that in dimension n any special orthogonal matrix R can be written as R = Q S QT, where Q is orthogonal and S is a block diagonal matrix with blocks of order 2, plus one of order 1 if n is odd; since each single block of order 2 is also an orthogonal matrix, it admits an exponential form. Correspondingly, the matrix S writes as exponential of a skew-symmetric block matrix Σ of the form above, S=exp(Σ), so that R = Q exp(Σ)QT = exp(Q Σ QT), exponential of the skew-symmetric matrix Q Σ QT. Conversely, the surjectivity of the exponential map, together with the above mentioned block-diagonalization for skew-symmetric matrices, implies the block-diagonalization for orthogonal matrices.