Size Function - Representation By Formal Series

Representation By Formal Series

An algebraic representation of size functions in terms of collections of points and lines in the real plane with multiplicities, i.e. as particular formal series, was furnished in, . The points (called cornerpoints) and lines (called cornerlines) of such formal series encode the information about discontinuities of the corresponding size functions, while their multiplicities contain the information about the values taken by the size function.

Formally:

  • cornerpoints are defined as those points, with, such that the number

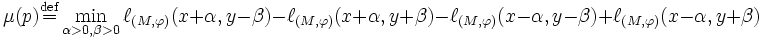\mu (p){\stackrel{{\rm def}}{=}}\min _{\alpha >0 ,\beta>0} \ell _{({M},\varphi )}(x+\alpha ,y- \beta)-\ell _{({ M},\varphi )} (x+\alpha ,y+\beta )- \ell_{({ M},\varphi )} (x-\alpha ,y-\beta )+\ell _{({ M} ,\varphi )} (x-\alpha ,y+\beta ) is positive. The number is said to be the multiplicity of .

  • cornerlines and are defined as those lines such that

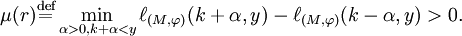\mu (r){\stackrel{\rm def}{=}}\min _{\alpha >0 ,k+\alpha <y}\ell _{({ M},\varphi )}(k+\alpha ,y)- \ell _{({ M},\varphi )}(k-\alpha ,y)>0. The number is sad to be the multiplicity of .

  • Representation Theorem: For every, it holds

This representation contains the same amount of information about the shape under study as the original size function does, but is much more concise.

This algebraic approach to size functions leads to the definition of new similarity measures between shapes, by translating the problem of comparing size functions into the problem of comparing formal series. The most studied among these metrics between size function is the matching distance.

Read more about this topic:  Size Function

Famous quotes containing the words formal and/or series:

    “The conviction that the best way to prepare children for a harsh, rapidly changing world is to introduce formal instruction at an early age is wrong. There is simply no evidence to support it, and considerable evidence against it. Starting children early academically has not worked in the past and is not working now.”
    —David Elkind (20th century)

    “Rosalynn said, “Jimmy, if we could only get Prime Minister Begin and President Sadat up here on this mountain for a few days, I believe they might consider how they could prevent another war between their countries.” That gave me the idea, and a few weeks later, I invited both men to join me for a series of private talks. In September 1978, they both came to Camp David.”
    —Jimmy Carter (James Earl Carter, Jr.)