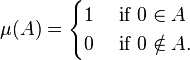Sigma Additivity - Examples

Examples

An example of a σ-additive function is the function μ defined over the power set of the real numbers, such that

\mu (A)= \begin{cases} 1 & \mbox{ if } 0 \in A \\ 0 & \mbox{ if } 0 \notin A. \end{cases}

If is a sequence of disjoint sets of real numbers, then either none of the sets contains 0, or precisely one of them does. In either case the equality

holds.

See measure and signed measure for more examples of σ-additive functions.

An example of an additive function which is not σ-additive is obtained by considering μ, defined over the power set of the real numbers by the slightly modified formula

\mu (A)= \begin{cases} \infty & \mbox { if } 0 \in \bar A \\ 0 & \mbox { if } 0 \notin \bar A \end{cases}

where the bar denotes the closure of a set.

One can check that this function is additive by using the property that the closure of a finite union of sets is the union of the closures of the sets, and looking at the cases when 0 is in the closure of any of those sets or not. That this function is not σ-additive follows by considering the sequence of disjoint sets

for n=1, 2, 3, ... The union of these sets is the interval (0, 1) whose closure is and μ applied to the union is then infinity, while μ applied to any of the individual sets is zero, so the sum of μ(An) is also zero, which proves the counterexample.

Read more about this topic:  Sigma Additivity

Famous quotes containing the word examples:

    “There are many examples of women that have excelled in learning, and even in war, but this is no reason we should bring ‘em all up to Latin and Greek or else military discipline, instead of needle-work and housewifry.”
    —Bernard Mandeville (1670–1733)

    “No rules exist, and examples are simply life-savers answering the appeals of rules making vain attempts to exist.”
    —André Breton (1896–1966)

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)