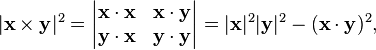Seven-dimensional Cross Product - Generalizations

Generalizations

Non-trivial binary cross products exist only in three and seven dimensions. But if the restriction that the product is binary is lifted, so products of more than two vectors are allowed, then more products are possible. As in two dimensions the product must be vector valued, linear, and anti-commutative in any two of the vectors in the product.

The product should satisfy orthogonality, so it is orthogonal to all its members. This means no more than n − 1 vectors can be used in n dimensions. The magnitude of the product should equal the volume of the parallelotope with the vectors as edges, which is can be calculated using the Gram determinant. So the conditions are

  • orthogonality:
  • the Gram determinant:
|\mathbf{a_1} \times \ \cdots \ \times \mathbf{a_k} |^2 = \det (\mathbf{a_i \cdot a_j}) = \begin{vmatrix} \mathbf {a_1 \cdot a_1} & \mathbf {a_1 \cdot a_2} & \dots & \mathbf {a_1 \cdot a_k}\\ \mathbf {a_2 \cdot a_1} & \mathbf {a_2 \cdot a_2} & \dots & \mathbf {a_2 \cdot a_k}\\ \dots & \dots & \dots & \dots\\ \mathbf {a_k \cdot a_1} & \mathbf {a_k \cdot a_2} & \dots & \mathbf {a_k \cdot a_k}\\ \end{vmatrix}

The Gram determinant is the squared volume of the parallelotope with a1, ..., ak as edges. If there are just two vectors x and y it simplifies to the condition for the binary cross product given above, that is

|\mathbf{x} \times \mathbf{y}|^2 = \begin{vmatrix} \mathbf {x \cdot x} & \mathbf {x \cdot y}\\ \mathbf {y \cdot x} & \mathbf {y \cdot y}\\ \end{vmatrix} = |\mathbf{x}|^2 |\mathbf{y}|^2 - (\mathbf{x} \cdot \mathbf{y})^2 ,

With these conditions a non-trivial cross product only exists:

  • as a binary product in three and seven dimensions
  • as a product of n − 1 vectors in n > 3 dimensions
  • as a product of three vectors in eight dimensions

The product of n − 1 vectors is in n dimensions is the Hodge dual of the exterior product of n − 1 vectors. One version of the product of three vectors in eight dimensions is given by

where v is the same trivector as used in seven dimensions, is again the left contraction, and w = −ve12...7 is a 4-vector.

Read more about this topic:  Seven-dimensional Cross Product