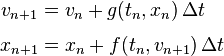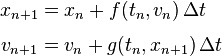Semi-implicit Euler Method - The Method

The Method

The semi-implicit Euler method produces an approximate discrete solution by iterating

\begin{align} v_{n+1} &= v_n + g(t_n, x_n) \, \Delta t\\ x_{n+1} &= x_n + f(t_n, v_{n+1}) \, \Delta t \end{align}

where Δt is the time step and tn = t0 + nΔt is the time after n steps.

The difference with the standard Euler method is that the semi-implicit Euler method uses vn+1 in the equation for xn+1, while the Euler method uses vn.

Applying the method with negative time step to the computation of from and rearranging leads to the second variant of the semi-implicit Euler method

\begin{align} x_{n+1} &= x_n + f(t_n, v_n) \, \Delta t\\ v_{n+1} &= v_n + g(t_n, x_{n+1}) \, \Delta t \end{align}

which has similar properties.

The semi-implicit Euler is a first-order integrator, just as the standard Euler method. This means that it commits a global error of the order of Δt. However, the semi-implicit Euler method is a symplectic integrator, unlike the standard method. As a consequence, the semi-implicit Euler method almost conserves the energy (when the Hamiltonian is time-independent). Often, the energy increases steadily when the standard Euler method is applied, making it far less accurate.

Alternating between the two variants of the semi-implicit Euler method leads in one simplification to the Störmer-Verlet integration and in a slightly different simplification to the leapfrog integration, increasing both the order of the error and the order of preservation of energy.

Read more about this topic:  Semi-implicit Euler Method

Famous quotes containing the word method:

    “Direct action ... is the logical, consistent method of Anarchism.”
    —Emma Goldman (1869–1940)

    “in the absence of feet, “a method of conclusions”;
    “a knowledge of principles,”
    in the curious phenomenon of your occipital horn.”
    —Marianne Moore (1887–1972)