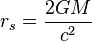Schwarzschild Geodesics - Schwarzschild Metric

Schwarzschild Metric

See also: Schwarzschild metric and Deriving the Schwarzschild solution

An exact solution to the Einstein field equations is the Schwarzschild metric, which corresponds to the external gravitational field of an uncharged, non-rotating, spherically symmetric body of mass M. The Schwarzschild solution can be written as

$c^2 {d \tau}^{2} = \left( 1 - \frac{r_{s}}{r} \right) c^{2} dt^{2} - \frac{dr^{2}}{1 - \frac{r_{s}}{r}} - r^{2} d\theta^{2} - r^{2} \sin^{2} \theta \, d\varphi^{2}$

where

τ is the proper time (time measured by a clock moving with the particle) in seconds,

c is the speed of light in meters per second,

t is the time coordinate (measured by a stationary clock at infinity) in seconds,

r is the radial coordinate (circumference of a circle centered on the star divided by 2π) in meters,

θ is the colatitude (angle from North) in radians,

φ is the longitude in radians, and

r_s is the Schwarzschild radius (in meters) of the massive body, which is related to its mass M by

$r_{s} = \frac{2GM}{c^{2}}$

where G is the gravitational constant. The classical Newtonian theory of gravity is recovered in the limit as the ratio r_s/r goes to zero. In that limit, the metric returns to that defined by special relativity.

In practice, this ratio is almost always extremely small. For example, the Schwarzschild radius r_s of the Earth is roughly 9 mm (3⁄₈ inch); at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The Schwarzschild radius of the Sun is much larger, roughly 2953 meters, but at its surface, the ratio r_s/r is roughly 4 parts in a million. A white dwarf star is much denser, but even here the ratio at its surface is roughly 250 parts in a million. The ratio only becomes large close to ultra-dense objects such as neutron stars (where the ratio is roughly 50%) and black holes.

Read more about this topic: Schwarzschild Geodesics